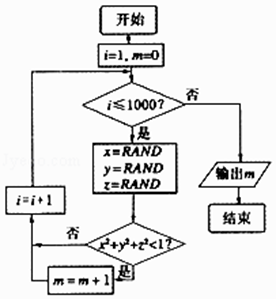
题目内容
【题目】已知函数f(x)=lnx﹣a(x﹣1),g(x)=ex .
(1)求函数f(x)的单调区间;
(2)当a≠0时,过原点分别作曲线y=f(x)与y=g(x)的切线l1 , l2 , 已知两切线的斜率互为倒数,证明: ![]() <a<
<a< ![]() ;
;
(3)设h(x)=f(x+1)+g(x),当x≥0,h(x)≥1时,求实数a的取值范围.
【答案】
(1)解:依题意,函数f(x)的定义域为(0,+∞),对f(x)求导,得 ![]() .
.
①若a≤0,对一切x>0有f'(x)>0,函数f(x)的单调递增区间是(0,+∞).
②若a>0,当 ![]() 时,f'(x)>0;当
时,f'(x)>0;当 ![]() 时,f'(x)<0.
时,f'(x)<0.
所以函数f(x)的单调递增区间是 ![]() ,单调递减区间是
,单调递减区间是 ![]()
(2)解:设切线l2的方程为y=k2x,切点为(x2,y2),则 ![]() ,
, ![]() ,
,
所以x2=1,y2=e,则 ![]() .
.
由题意知,切线l1的斜率为 ![]() ,l1的方程为
,l1的方程为 ![]() .
.
设l1与曲线y=f(x)的切点为(x1,y1),则 ![]() ,
,
所以 ![]() ,
, ![]() .
.
又因为y1=lnx1﹣a(x1﹣1),消去y1和a后,整理得 ![]() . (6分)
. (6分)
令 ![]() ,则
,则 ![]() ,m(x)在(0,1)上单调递减,在(1,+∞)上单调递增.
,m(x)在(0,1)上单调递减,在(1,+∞)上单调递增.
若x1∈(0,1),因为 ![]() ,
, ![]() ,所以
,所以 ![]() ,
,
而 ![]() 在
在 ![]() 上单调递减,所以
上单调递减,所以 ![]() .
.
若x1∈(1,+∞),因为m(x)在(1,+∞)上单调递增,且m(e)=0,则x1=e,
所以 ![]() (舍去).
(舍去).
综上可知, ![]()
(3)解:证明:h(x)=f(x+1)+g(x)=ln(x+1)﹣ax+ex, ![]() .
.
①当a≤2时,因为ex≥x+1,所以 ![]() ,h(x)在[0,+∞)上递增,h(x)≥h(0)=1恒成立,符合题意.
,h(x)在[0,+∞)上递增,h(x)≥h(0)=1恒成立,符合题意.
②当a>2时,因为 ![]() ,所以h′(x)在[0,+∞)上递增,且h′(0)=2﹣a<0,则存在x0∈(0,+∞),使得h′(0)=0.
,所以h′(x)在[0,+∞)上递增,且h′(0)=2﹣a<0,则存在x0∈(0,+∞),使得h′(0)=0.
所以h(x)在(0,x0)上递减,在(x0,+∞)上递增,又h(x0)<h(0)=1,所以h(x)≥1不恒成立,不合题意.综合①②可知,所求实数a的取值范围是(﹣∞,2]
【解析】(1)利用导数求函数的单调区间,注意对参数a的分类讨论;(2)背景为指数函数y=ex与对数函数y=lnx关于直线y=x对称的特征,得到过原点的切线也关于直线y=x对称,主要考查利用导函数研究曲线的切线及结合方程有解零点存在定理的应该用求参数的问题,得到不等式的证明;(3)考查利用导数处理函数的最值和不等式的恒成立求参数的范围问题,求导过程中用到了课后习题ex≥x+1这个结论,考查学生对课本知识的掌握程度.

 阅读快车系列答案
阅读快车系列答案【题目】某兴趣小组欲研究昼夜温差大小与患感冒人数多少之间的关系,他们分别到气象局与某医院抄录了![]() 至
至![]() 月份每月
月份每月![]() 号的昼夜温差情况与因患感冒而就诊的人数,得到如下资料:
号的昼夜温差情况与因患感冒而就诊的人数,得到如下资料:
日期 | 1月10日 | 2月10日 | 3月10日 | 4月10日 | 5月10日 | 6月10日 |
昼夜温差
|
|
|
|
|
|
|
就诊人数 |
|
|
|
|
|
|
该兴趣小组确定的研究方案是:先从这六组数据中选取![]() 组,用剩下的
组,用剩下的![]() 组数据求线性回归方程,再用被选取的
组数据求线性回归方程,再用被选取的![]() 组数据进行检验.
组数据进行检验.
(1)求选取的![]() 组数据恰好是相邻两月的概率;
组数据恰好是相邻两月的概率;
(2)若选取的是1月与![]() 月的两组数据,请根据2至5月份的数据,求出
月的两组数据,请根据2至5月份的数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(3)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过![]() 人,则认为得到的线性回归方程是理想的,试问该小组所得线性回归方程是否理想?
人,则认为得到的线性回归方程是理想的,试问该小组所得线性回归方程是否理想?
参考数据![]() ,
,![]()
(参考公式: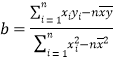
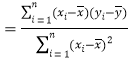 ,
,![]() )
)
【题目】在统计学中,偏差是指个别测定值与测定的平均值之差,在成绩统计中,我们把某个同学的某科考试成绩与该科班平均分的差叫某科偏差,班主任为了了解个别学生的偏科情况,对学生数学偏差x(单位:分)与物理偏差y(单位:分)之间的关系进行学科偏差分析,决定从全班56位同学中随机抽取一个容量为8的样本进行分析,得到他们的两科成绩偏差数据如下:
学生序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
数学偏差x | 20 | 15 | 13 | 3 | 2 | -5 | -10 | -18 |
物理偏差y | 6.5 | 3.5 | 3.5 | 1.5 | 0.5 | -0.5 | -2.5 | -3.5 |
(1)已知x与y之间具有线性相关关系,求y关于x的线性回归方程;
(2)若这次考试该班数学平均分为118分,物理平均分为90.5,试预测数学成绩126分的同学的物理成绩.
参考公式:  ,.
,.![]()
参考数据: ![]() .
.