题目内容
14.已知函数f(x)=$\frac{3x}{a}$-2x2+lnx(a∈R且a≠0),当a=3时,求函数的单调区间.分析 化简函数f(x)=x-2x2+lnx,从而求导f′(x)=1-4x+$\frac{1}{x}$=$\frac{-4{x}^{2}+x+1}{x}$=-$\frac{(x-\frac{1-\sqrt{17}}{8})(x-\frac{1+\sqrt{17}}{8})}{x}$,从而确定函数的单调区间.
解答 解:当a=3时,
f(x)=x-2x2+lnx的定义域为(0,+∞),
f′(x)=1-4x+$\frac{1}{x}$=$\frac{-4{x}^{2}+x+1}{x}$
=-$\frac{(x-\frac{1-\sqrt{17}}{8})(x-\frac{1+\sqrt{17}}{8})}{x}$,
故当x∈(0,$\frac{1+\sqrt{17}}{8}$)时,f′(x)>0,
当x∈($\frac{1+\sqrt{17}}{8}$,+∞)时,f′(x)<0,
故函数的单调增区间为(0,$\frac{1+\sqrt{17}}{8}$),
单调减区间为($\frac{1+\sqrt{17}}{8}$,+∞).
点评 本题考查了导数的综合应用及函数的单调区间的求法.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6.如图,在三棱锥V-ABC,VA=VC,VB⊥AC,则AB与BC的大小关系是( )
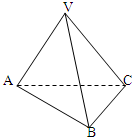

| A. | AB>BC | B. | AB=BC | C. | AB<BC | D. | 无法确定 |
4.下列命题中是真命题的是( )
| A. | 函数y=sin2x的最小正周期是2π | B. | 等差数列一定是单调数列 | ||
| C. | 直线y=ax+a过定点(-1,0) | D. | 在△ABC中,若sinB>0,则B为锐角 |