题目内容
已知函数y=f(x)=![]() (a,b,c∈R,a>0,b>0)是奇函数,当x>0时,f(x)有最小值2,其中b∈N且f(1)<
(a,b,c∈R,a>0,b>0)是奇函数,当x>0时,f(x)有最小值2,其中b∈N且f(1)<![]() .
.
(1)试求函数f(x)的解析式;
(2)问函数f(x)图象上是否存在关于点(1,0)对称的两点,若存在,求出点的坐标;若不存在,说明理由.
(1) f(x)=x+![]() .
.
(2) y=f(x)图象上存在两点(1+![]() ,2
,2![]() ),(1-
),(1-![]() ,-2
,-2![]() )关于(1,0)对称.
)关于(1,0)对称.
解析:
(1)∵f(x)是奇函数,∴f(-x)=-f(x),即![]()
∴c=0,∵a>0,b>0,x>0,∴f(x)=![]() ≥2
≥2![]() ,当且仅当x=
,当且仅当x=![]() 时等号成立,于是2
时等号成立,于是2![]() =2,∴a=b2,由f(1)<
=2,∴a=b2,由f(1)<![]() 得
得![]() <
<![]() 即
即![]() <
<![]() ,∴2b2-5b+2<0,解得
,∴2b2-5b+2<0,解得![]() <b<2,又b∈N,∴b=1,∴a=1,∴f(x)=x+
<b<2,又b∈N,∴b=1,∴a=1,∴f(x)=x+![]() .
.
(2)设存在一点(x0,y0)在y=f(x)的图象上,并且关于(1,0)的对称点(2-x0,-y0)也在y=f(x)图象上,则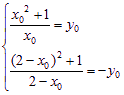
消去y0得x02-2x0-1=0,x0=1±![]() .
.
∴y=f(x)图象上存在两点(1+![]() ,2
,2![]() ),(1-
),(1-![]() ,-2
,-2![]() )关于(1,0)对称.
)关于(1,0)对称.

练习册系列答案
相关题目
已知函数y=f(x+
)为奇函数,设g(x)=f(x)+1,则g(
)+g(
)+g(
)+g(
)+…+g(
)=( )
| 1 |
| 2 |
| 1 |
| 2011 |
| 2 |
| 2011 |
| 3 |
| 2011 |
| 4 |
| 2011 |
| 2010 |
| 2011 |
| A、1005 | B、2010 |
| C、2011 | D、4020 |