题目内容
6.已知$\overrightarrow a=({-1,2})$,$\overrightarrow b=({1,λ})$,且$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为钝角,则实数λ的取值范围是$({-∞,-2})∪({-2,\frac{1}{2}})$.分析 两个不共线向量夹角为钝角的充分必要条件是它们的数量积小于零.由此可根据数量积的公式,列出不等式组,可得到实数λ的取值范围
解答 解:因为$\overrightarrow a=({-1,2})$,$\overrightarrow b=({1,λ})$,且$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为钝角
所以$\left\{\begin{array}{l}{-1×1+2λ<0}\\{-1×λ-2×1≠0}\end{array}\right.$解得$λ<\frac{1}{2}$且λ≠-2;
故答案为:$({-∞,-2})∪({-2,\frac{1}{2}})$.
点评 本题考查了向量的数量积公式;特别注意;向量夹角为钝角不等价它们的数量积小于0 (当向量反向时,数量积也小于0).

练习册系列答案
相关题目
16.设i是虚数单位,若复数$z=\frac{{{a^2}+ai}}{1-i}>0$,则a的值为( )
| A. | 0或-1 | B. | 0或1 | C. | -1 | D. | 1 |
17.已知$\frac{a+3i}{i}$=b+i(a,b∈R,i为虚数单位),则a+b等于( )
| A. | -4 | B. | -2 | C. | 2 | D. | 4 |
18.若向量$\overrightarrow{a}$=(2,x+1),$\overrightarrow{b}$=(x+2,6),又$\overrightarrow{a}$,$\overrightarrow{b}$的夹角为锐角,则实数x的取值范围为( )
| A. | {x|x>-$\frac{5}{4}$且x≠2} | B. | {x|x>-$\frac{5}{4}$} | C. | {x|x<-$\frac{5}{4}$且x≠-5} | D. | {x|x<-$\frac{5}{4}$} |
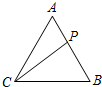 如图,在等边三角形ABC中,P在线段AB上,且$\overrightarrow{AP}=λ\overrightarrow{AB}$,其中0<λ<1,若$\overrightarrow{PA}•\overrightarrow{PB}+\overrightarrow{PC}•\overrightarrow{AB}$=0,则λ的值为$\frac{{2-\sqrt{2}}}{2}$.
如图,在等边三角形ABC中,P在线段AB上,且$\overrightarrow{AP}=λ\overrightarrow{AB}$,其中0<λ<1,若$\overrightarrow{PA}•\overrightarrow{PB}+\overrightarrow{PC}•\overrightarrow{AB}$=0,则λ的值为$\frac{{2-\sqrt{2}}}{2}$.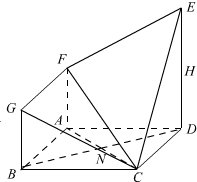 在如图所示的几何体ABCDEFG中,四边形ABCD是边长为4的正方形,DE⊥平面ABCD,DE∥AF∥BG,H是DE的中点,AC与BD相交于N,DE=2AF=2BG=4
在如图所示的几何体ABCDEFG中,四边形ABCD是边长为4的正方形,DE⊥平面ABCD,DE∥AF∥BG,H是DE的中点,AC与BD相交于N,DE=2AF=2BG=4