题目内容
6. (1)金刚石和石墨的晶胞如图,若碳原子半径为a cm 且相邻最近的碳原子相切,阿伏加德罗常数为NA,则金刚石的密度表达式为(要求整理为分母不含根号的表达式)$\frac{9\sqrt{3}}{1{6a}^{3}{N}_{A}}$g/cm3,一个石墨晶胞内含有4个碳原子,石墨的熔点比金刚石的熔点要高,其原因是石墨中碳碳键长小于金刚石中碳碳键长,这两种晶胞中碳的配位数(每个碳周围与之最近的碳原子数)之比为4:3.
(1)金刚石和石墨的晶胞如图,若碳原子半径为a cm 且相邻最近的碳原子相切,阿伏加德罗常数为NA,则金刚石的密度表达式为(要求整理为分母不含根号的表达式)$\frac{9\sqrt{3}}{1{6a}^{3}{N}_{A}}$g/cm3,一个石墨晶胞内含有4个碳原子,石墨的熔点比金刚石的熔点要高,其原因是石墨中碳碳键长小于金刚石中碳碳键长,这两种晶胞中碳的配位数(每个碳周围与之最近的碳原子数)之比为4:3.(2)分子筛是一类具有骨架结构的硅铝酸盐晶体,实验式表示为
M${\;}_{\frac{2}{n}}$O•xA12O3•ySiO2,M是金属离子(可为Na、K、Ca等金属离子),n是M的价数,其最基本的结构单位是硅氧和铝氧四面体.因为硅是+4价,氧是-2价,因此,硅和氧的化合价都得到满足,因为铝是+3价,故铝氧四面体带有1个负电荷,金属离子用以保持电中性.某分子筛铝硅比(铝原子与硅原子的个数比)和钾钠比均为2,则其化学式:2K2O•Na2O•3A12O3•3SiO2,其中铝的杂化方式sp3.
分析 (1)根据均摊法计算晶胞中C原子数目,用NA表示出晶胞的质量.金刚石中每个碳原子与周围4个碳原子形成正四面体结构,四面体中心原子与顶点原子相邻,则四面体中心到顶点距离为2a cm,到底面距离为$\frac{2a}{3}$cm,设四面体棱长为y,则侧面高为$\frac{\sqrt{3}}{2}$y,底面中心到边的距离为$\frac{\sqrt{3}}{2}$y×$\frac{1}{3}$,故(a cm+$\frac{2a}{3}$cm)2+($\frac{\sqrt{3}}{2}$y×$\frac{1}{3}$)2=($\frac{\sqrt{3}}{2}$y)2,整理得y=$\frac{4\sqrt{6}}{3}$a cm,故晶胞棱长=$\frac{4\sqrt{6}}{3}$a cm×2×$\frac{\sqrt{2}}{2}$=$\frac{8\sqrt{3}}{3}$a cm,进而计算晶胞体积,再根据ρ=$\frac{m}{V}$计算晶胞密度;
金刚石晶胞中C原子个数=8×$\frac{1}{8}$+6×$\frac{1}{2}$+4=8,距离最近的碳原子为顶点上的C原子和在晶胞内部直接与该顶点原子相邻的原子,二者之间距离为2acm,2acm为晶胞体长的$\frac{1}{4}$,则晶胞棱长=$\sqrt{\frac{(2a×4)^{2}}{3}}$cm=$\frac{8a\sqrt{3}}{3}cm$,根据均摊法计算石墨晶胞中碳原子数目,石墨中碳碳键长小于金刚石中碳碳键长导致石墨熔点较高;
金刚石中碳原子配位数是4,石墨中碳原子配位数是3;
(2)分子筛属于硅铝酸盐晶体,铝硅比(铝原子与硅原子的个数比)和钾钠比均为2,可以设化学式为:2xK2O•xNa2O•yA12O3•ySiO2,1mol该晶体含有2y mol铝氧四面体,由电荷守恒可知确定x、y关系,进而确定化学式;
基本的结构单位是硅氧和铝氧四面体,因为硅是+4价,氧是-2价,硅和氧的化合价都得到满足,因为铝是+3价,故铝氧四面体带有1个负电荷,则Al与氧原子之间形成4对电子对,其中一个为Al氧原子与氧离子形成的配位键(每个氧离子参与形成2个铝氧四面体,即形成2个配位键,铝氧四面体带有1个负电荷),即Al原子形成4个σ键,没有孤电子对.
解答 解:(1)金刚石晶胞中C原子个数=8×$\frac{1}{8}$+4+6×$\frac{1}{2}$=8,则晶胞质量为$\frac{8×12}{{N}_{A}}$g,金刚石中每个碳原子与周围4个碳原子形成正四面体结构,四面体中心原子与顶点原子相邻,则四面体中心到顶点距离为2a cm,到底面距离为$\frac{2a}{3}$cm,设四面体棱长为y,则侧面高为$\frac{\sqrt{3}}{2}$y,底面中心到边的距离为$\frac{\sqrt{3}}{2}$y×$\frac{1}{3}$,故(a cm+$\frac{2a}{3}$cm)2+($\frac{\sqrt{3}}{2}$y×$\frac{1}{3}$)2=($\frac{\sqrt{3}}{2}$y)2,整理得y=$\frac{4\sqrt{6}}{3}$a cm,故晶胞棱长=$\frac{4\sqrt{6}}{3}$a cm×2×$\frac{\sqrt{2}}{2}$=$\frac{8\sqrt{3}}{3}$a cm,则晶胞密度为$\frac{8×12}{{N}_{A}}$g÷($\frac{8\sqrt{3}}{3}$a cm)3=$\frac{9\sqrt{3}}{1{6a}^{3}{N}_{A}}$g/cm3;
一个石墨晶胞中C原子个数=8×$\frac{1}{8}$+1+2×$\frac{1}{2}$+4×$\frac{1}{4}$=4;
石墨中碳碳键长小于金刚石中碳碳键长,导致石墨熔点较高;
金刚石中碳原子配位数是4,石墨中碳原子配位数是3,配位数之比为4:3,
故答案为:$\frac{9\sqrt{3}}{1{6a}^{3}{N}_{A}}$;4;石墨中碳碳键长小于金刚石中碳碳键长;4:3;
(2)分子筛属于硅铝酸盐晶体,铝硅比(铝原子与硅原子的个数比)和钾钠比均为2,可以设化学式为:2xK2O•xNa2O•yA12O3•ySiO2,1mol该晶体含有2y mol铝氧四面体,由电荷守恒可知:4x+2x=2y,故y=3x,则化学式为:2K2O•Na2O•3A12O3•3SiO2;
基本的结构单位是硅氧和铝氧四面体,因为硅是+4价,氧是-2价,硅和氧的化合价都得到满足,因为铝是+3价,故铝氧四面体带有1个负电荷,则Al与氧原子之间形成4对电子对,其中一个为Al氧原子与氧离子形成的配位键(每个氧离子参与形成2个铝氧四面体,即形成2个配位键,铝氧四面体带有1个负电荷),即Al原子形成4个σ键,没有孤电子对,Al原子采取sp3杂化,
故答案为:2K2O•Na2O•3A12O3•3SiO2;sp3.
点评 本题考查晶胞结构及晶胞计算,需要学生具备一定空间想象与数学计算能力,(2)中关键是理解铝氧四面体的结构,综合考查学生分析理解能力,难度较大.

 阅读快车系列答案
阅读快车系列答案| A. | NO2 | B. | SO2 | C. | SO3 | D. | CO2 |
x?Y
| 物质 选项 | X | Y |
| A | Na2CO3 | NaHCO3 |
| B | Al(OH)3 | Al2O3 |
| C | FeCl3 | FeCl2 |
| D | CuSO4 | Cu(OH)2 |
| A. | A | B. | B | C. | C | D. | D |
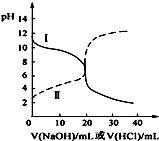 25℃时,取浓度均为0.1mol•L-1的醋酸溶液和氨水溶液各20mL,分别用0.1mol•L-1NaOH溶液、0.1mol•L-1盐酸进行中和滴定,滴定过程中pH随滴加溶液的体积变化关系如图所示.下列说法正确的是( )
25℃时,取浓度均为0.1mol•L-1的醋酸溶液和氨水溶液各20mL,分别用0.1mol•L-1NaOH溶液、0.1mol•L-1盐酸进行中和滴定,滴定过程中pH随滴加溶液的体积变化关系如图所示.下列说法正确的是( )| A. | 曲线Ⅰ:滴加溶液到10mL时:c(CH3COO-)>c(Na+)>c(H+)>c(OH-) | |
| B. | 曲线Ⅱ:滴加溶液到10 mL时:c(CH3COO-)-c(CH3COOH)=2[c(OH-)-c(H+)] | |
| C. | 曲线Ⅱ:滴加溶液在10 mL~20 mL之间存在:c(NH4+)=c(Cl-)>c(OH-)=c(H+) | |
| D. | 曲线Ⅰ:滴加溶液到20 mL时:c(Cl-)>c(NH4+)>c(H+)>c(NH3•H2O)>c(OH-) |
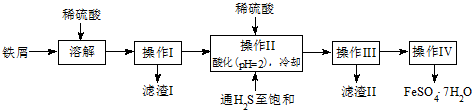
查询资料,得25℃时有关物质的数据如下表:
| 饱和H2S溶液 | SnS沉淀完全 | FeS开始沉淀 | FeS沉淀完全 | |
| pH值 | 3.9 | 1.6 | 3.0 | 5.5 |
(2)操作Ⅳ得到的绿矾晶体用少量冰水洗涤,其目的是:
①除去晶体表面附着的硫酸等杂质;②降低洗涤过程中FeSO4•7H2O的损耗.
(3)工业上常用氧化还原滴定法测定绿矾产品中Fe2+含量,测定步骤如下:
a.称取2.850g绿矾产品,溶解,在250mL容量瓶中定容;
b.量取25.00mL待测溶液于锥形瓶中;
c.用硫酸酸化的0.01000mol•L-1KMnO4溶液滴定至终点,消耗KMnO4溶液体积的平均值为20.00mL.
①已知酸性KMnO4被FeSO4还原时生成Mn2+.写出该测定过程的离子反应方程式:MnO4-+5Fe2++8H+=Mn2++5Fe3++4H2O;
②滴定时盛放KMnO4溶液的仪器为酸式滴定管(填仪器名称).
③判断此滴定实验达到终点的方法是滴加最后一滴KMnO4溶液时,溶液变成浅红色且半分钟内不褪色.
④若实验操作无失误,测得上述样品中FeSO4•7H2O的含量仍偏低,则可能的原因是:部分Fe2+被空气中O2氧化.
| A. | 在涂料中尽量用液态有机物代替水作溶剂,以减少环境污染 | |
| B. | 向煤中加入适量石灰石,在煤燃烧时SO2最终生成CaSO4,可减少对大气的污染 | |
| C. | “海水淡化”可以解决“淡水供应危机”,加入明矾可以使海水淡化 | |
| D. | 食物溶于水后的溶液 pH<7,则该食物为成酸性食物 |
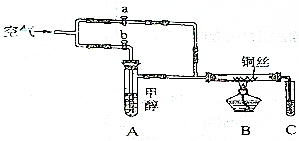 如图所示装置,通入空气,开启a、b两个活塞,灼热铜丝,下列有关分析正确的是( )
如图所示装置,通入空气,开启a、b两个活塞,灼热铜丝,下列有关分析正确的是( )| A. | 灼热铜丝发生的现象变化为紫红色和黑色交替出现,甲醇发生还原反应 | |
| B. | C中有机产物易溶于水,与水分子间只形成1种氢键 | |
| C. | 检验C中产物的试剂可用1mol•L-1的CuSO4溶液2mL和0.4mol•L-1的NaOH | |
| D. | 可用酸性高锰酸钾溶液检验产物生成 |
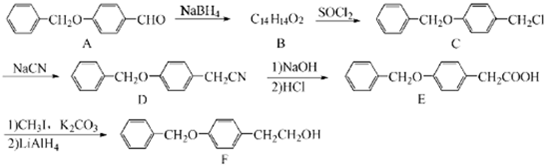
 ;由C→D的反应类型是:取代反应.
;由C→D的反应类型是:取代反应. .
. 为原料制备化合物X(结构简式见图)的合成路线流程图(无机试剂可任选).合成路线流程图示例如图:CH3CHO$→_{催化剂△}^{O_{2}}$CH3COOH$→_{浓硫酸△}^{CH_{3}CH_{2}OH}$CH3COOCH2CH3.
为原料制备化合物X(结构简式见图)的合成路线流程图(无机试剂可任选).合成路线流程图示例如图:CH3CHO$→_{催化剂△}^{O_{2}}$CH3COOH$→_{浓硫酸△}^{CH_{3}CH_{2}OH}$CH3COOCH2CH3.
