Question

【题目】归纳式探究﹣﹣探究小球沿过山车轨道的运动 小雨观察到游乐场的过山车可以底朝上在圆形轨道上运动，游客却不会掉下来．他想探索其中的奥秘，做了以下两个探究：

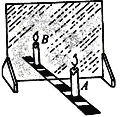
（1）探究一：如图甲所示，小球由A点沿光滑轨道自由运动到B点，小球到达B点的速度v与高度h和小球质量m的关系，数据如表一． 表一：

实验次数	h/m	m/kg	v2/（m2s﹣2）
1	0.2	2.0×10﹣2	4.0
2	0.4	2.0×10﹣2	8.0
3	0.4	3.0×10﹣2	8.0
4	0.8	2.5×10﹣2	16.0

则小球到达B点的速度v与有关，且v2=k1 ．
（2）探究二：如图乙所示，小球以一定速度从B点沿光滑的竖直圆形轨道运动，恰好通过最高点C．小球在B点的速度v与轨道半径r的关系，数据如表二．

实验次数	r/m	v2/（m2s﹣2）
1	0.15	7.5
2	0.30	15.0
3	0.45	22.5

则小球在B点的速度v与轨道半径r的关系式为 ．
（3）如图丙所示，将甲、乙两轨道组合后，小球从A点沿光滑轨道自由运动，若r=0.4m，要使小球经过B点后能恰好通过C点，则h= ．

Answer 1

【答案】
（1）高度h；h
（2）v2=50m/s2×r
（3）1m
【解析】解：（1）表格一：由1、2次实验数据可知，质量相同时，下滑的高度越高到达B点速度的平方越大，且小球下落高度的倍数和到达B点速度平方的倍数相等，即小球到达B点的速度v的平方与高度h成正比； 由2、3次实验数据可知，小球下滑的高度相同时，质量不同的小球到达B点速度的平方相等，则小球到达B点的速度与小球的质量无关，
综上可知，小球到达B点的速度v与高度h有关，且v2=k1h．（2）表格二：
由三次实验数据可知，轨道半径的变化数据和v2的变化倍数相等，则小球在B点的速度v2与轨道半径r成正比，设为v2=kr，
把v2=7.5m2/s2、r=0.15m代入可得，k=50m/s2 ，
小球在B点的速度v与轨道半径r的关系式为v2=50m/s2×r；（3）由表格一数据可知，当v2=4.0m2/s2时h=0.2m，
则k1= =20m/s2 ，
小球从A点沿光滑轨道自由运动，恰好通过C点时，
由v2=50m/s2×r可得，B点的速度平方：
vB2=50m/s2×r=50m/s2×0.4m=20m2/s2 ，
由v2=k1h可得，小球下落的高度：
hB= =1m．
所以答案是：（1）高度h；h；（2）v2=50m/s2×r；（3）1m．