��Ŀ����
����Ŀ����ͼ�ǡ�̽��ƽ�澵�����ص㡱���龰�����������������·���һ��ֱ�ߣ�ֱ���벣���崹ֱ����֧��ͬ������A��B�����ڲ����������ֱ���ϣ���A����Ϊ��������
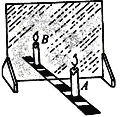
��Ϊ���ڹ۲죬��ʵ�������_______�����н��У�ѡ����������Ϻڰ����������⣬���������������ƽ�澵����Ȼ������ƽ�澵��������ȴ���ڹ۲쵽A�������ͬʱ��Ҳ�ܹ۲쵽______________������ؽ����ȷ�����λ�úʹ�С������
�Ƶ�ȼA����С�ĵ��ƶ�B����ֱ����A��������غ�Ϊֹ����ʱ����������Ĵ�С_______����һ���۲�A��B��֧������ֱ���ϵ�λ�÷��֣������������벣����_______������ﵽ������ľ���_______.
���𰸡� �Ϻڰ� B���� ��� ��ֱ ���
����������1����ȼ���������������Ļ����У���������������ԱȶȽ�С������̫�����������ںڰ������У�����ͺڰ������ĶԱȶȴ�������������Ը�ʵ������ڽϺڰ������н��У�ʵ������У������IJ��������ƽ�澵��������һ�࣬���ܿ�������A����Ҳ�ܿ�����������A������B��������A���������B�غ�ʱ������ȷ�����λ�ã����ڱȽ������С����2����ȼA����С�ĵ��ƶ�B����ֱ����A��������غ�Ϊֹ����ʱ����������Ĵ�С��ȣ���һ���۲�A��B��֧������ֱ���ϵ�λ�÷��֣������������벣���崹ֱ������ﵽ������ľ�����ȣ�

 ��ĩ���100�ִ��½����ȫ�Ծ�ϵ�д�
��ĩ���100�ִ��½����ȫ�Ծ�ϵ�д�����Ŀ���ع�ʵ���̽�����뽫����ʵ�鱨���еĿ�ȱ������д��������
��1��̽���ܶȸ���Ľ�����
����ͼ�� |
| �����ñ����е����ݣ�����㷨���������m-Vͼ��. | ||||||||||||
���� | ͬ�����ʵ�����������ı�ֵ���ģ� | |||||||||||||
�������� | С������ƽ����Ͳ�������ϵ��ܶȣ����õĿ�ѧ��������������ʵ�鲽�����£�������ƽ������ձ�������m0��������Ͳ������ϵ����V���۰����ϴ���Ͳ������ձ�������ձ������ϵ�������m1���ܴ��빫ʽ��= | |||||||||||||
��2��̽��Ӱ�컬��Ħ������С�����أ�
���� | С����룺�ڽӴ���ֲڳ̶���ͬʱ������Ħ�����Ĵ�С��ѹ����С���ٶȴ�С�йأ� |
���� | Ҷ�ӽ����ΪС��IJ��벻�ԣ����ǽ���������ʵ�飺 |
���� | ������⩁������ʵ�鷴�������ó����ۣ� |
��ͼ | ����ͼ����ľ����ˮƽ��������������ʾ��ͼ �� |
���� | ��һ���ֱ�ñ�����ھ�ֹ��ľ���ϣ�ͻȻ��������ľ�飬���ֱָ�ñ�㵹������ҡ�����������˵��������й��ԣ� |
����Ŀ������ʽ̽������̽��С���ع�ɽ��������˶� С��۲쵽���ֳ��Ĺ�ɽ�����Ե׳�����Բ�ι�����˶����ο�ȴ���������������̽�����еİ��أ�������������̽����
��1��̽��һ����ͼ����ʾ��С����A���ع⻬��������˶���B�㣬С��B����ٶ�v��߶�h��С������m�Ĺ�ϵ���������һ�� ��һ��
ʵ����� | h/m | m/kg | v2/��m2s��2�� |
1 | 0.2 | 2.0��10��2 | 4.0 |
2 | 0.4 | 2.0��10��2 | 8.0 |
3 | 0.4 | 3.0��10��2 | 8.0 |
4 | 0.8 | 2.5��10��2 | 16.0 |
��С��B����ٶ�v���йأ���v2=k1 ��
��2��̽��������ͼ����ʾ��С����һ���ٶȴ�B���ع⻬����ֱԲ�ι���˶���ǡ��ͨ����ߵ�C��С����B����ٶ�v�����뾶r�Ĺ�ϵ�������������
ʵ����� | r/m | v2/��m2s��2�� |
1 | 0.15 | 7.5 |
2 | 0.30 | 15.0 |
3 | 0.45 | 22.5 |
��С����B����ٶ�v�����뾶r�Ĺ�ϵʽΪ ��
��3����ͼ����ʾ�����ס����������Ϻ�С���A���ع⻬��������˶�����r=0.4m��ҪʹС��B�����ǡ��ͨ��C�㣬��h= ��
����Ŀ����ͼ��ʾ�ǡ�̽��������ʵ���װ�ã�ʵ��ʱ���ȵ������桢�����������ߵ����Ĵ�����ͬһ�߶��ϣ�Ȼ�ϸı��������ľ��룬���ƶ�������λ�ã��õ���ʵ�����������
ʵ����� | ��� | ��� | ������� | ||
���� | ��С | ��ʵ | |||
1 | 40 | 13.3 | ���� | ��С | ʵ�� |
2 | 30 | 15 | ���� | ��С | ʵ�� |
3 | 20 | 20 | ���� | �Ŵ� | ʵ�� |
4 | 15 | 30 | ���� | �Ŵ� | ʵ�� |
5 | 12 | 60 | ���� | �Ŵ� | ʵ�� |
6 | 10 |
| ������ | ||
7 | 8 |
| ���� | �Ŵ� | ���� |
8 | 4 |
| ���� | �Ŵ� | ���� |
��1��ͼ������ʾ��ʵ�����Ŀ����ʲô��
��2��ʵ������У��۲쵽��������λ�õı仯����ı仯������ת�۵㣬�����������ݾ���Ϊ������ת�۵��λ���ںδ������Ƿֱ���������ֱ仯���̵�ת�۵㣿












