题目内容
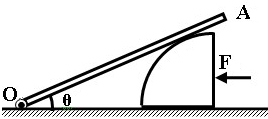 如图所示,横截面为四分之一圆(半径为R)的柱体放在水平地面上,一根匀质木棒OA长为3R,重为G.木棒的O端与地面上的铰链连接,木棒搁在柱体上,各处摩擦均不计.现用一水平推力F作用在柱体竖直面上,使柱体沿着水平地面向左缓慢移动.问:
如图所示,横截面为四分之一圆(半径为R)的柱体放在水平地面上,一根匀质木棒OA长为3R,重为G.木棒的O端与地面上的铰链连接,木棒搁在柱体上,各处摩擦均不计.现用一水平推力F作用在柱体竖直面上,使柱体沿着水平地面向左缓慢移动.问:
(1)当木棒与地面的夹角θ=30°时,柱体对木棒的弹力多大?
(2)此时水平推力F多大?
(3)在柱体向左缓慢移动过程中,柱体对木棒的弹力及水平推力F分别如何变化?
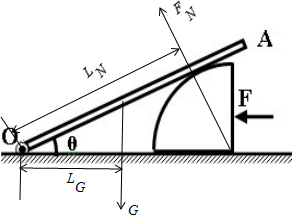 解:(1)如图示,重力的力臂LG=
解:(1)如图示,重力的力臂LG= cosθ=
cosθ= cos30°=
cos30°= ×
× =
=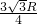 ,柱体与木棒的弹力力臂LN=
,柱体与木棒的弹力力臂LN=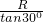 =
= R,
R,由杠杆的平衡条件,得:GLG=FNLN,FN=
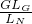 =
= =
=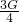
(2)柱体在水平方向受水平向左的推力F,水平向右的木棒对柱体压力的水平分力F1=FNsinθ=FNsin30°=
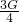 ×
× =
=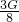 .
.柱体缓慢移动可认为柱体在水平方向平衡,由平衡条件得:F=F1=
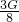 .
.(3)由(1)知LN=
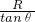 ,GLG=FNLN,FN=
,GLG=FNLN,FN=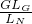 =
=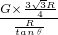 =
=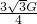 tanθ,在柱体缓慢向左移动的过程中,θ不断变大,从而tanθ不断变大,FN不断变大.
tanθ,在柱体缓慢向左移动的过程中,θ不断变大,从而tanθ不断变大,FN不断变大.在水平方向上,水平推力F=FNsinθ,在柱体缓慢向左移动的过程中,θ不断变大,sinθ不断增大,FN不断变大,所以F不断变大.
答:(1)柱体对木棒的弹力为
 G.(2)此时水平推力为
G.(2)此时水平推力为 G.(3)在柱体向左缓慢移动过程中,柱体对木棒的弹力及水平推力F都不断变大.
G.(3)在柱体向左缓慢移动过程中,柱体对木棒的弹力及水平推力F都不断变大.分析:(1)先求出柱体与木棒间弹力的力臂LN,木棒重力的力臂LG,然后根据杠杆平衡条件:GLG=FNLN求弹力.
(2)柱体在水平方向受推力F及木棒压力的分力F1,在这两个力的作用下柱体处于平衡状态,平衡条件可求出水平推力.
(3)先求出弹力LN及推力F大小的表达式,然后由数学知识tanθ,sinθ,随θ的增加而增大,来判断FN,F大小如何变化.
点评:本题考查了:(1)杠杆平衡问题,求柱体对木棒弹力的关键是,准确地求出各力的力臂.
(2)物体的动态平衡问题,解此类题时先求出各力的表达式,再由数学知识讨论力如何变化.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
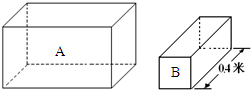 (2011?嘉定区一模)如图所示,横截面为正方形的实心均匀长方体A、B放置在水平地面上,它们的高度分别为0.2米和0.1米,B的另一条边长为0.4米,A的密度为2×103千克/米3,B质量为1千克.
(2011?嘉定区一模)如图所示,横截面为正方形的实心均匀长方体A、B放置在水平地面上,它们的高度分别为0.2米和0.1米,B的另一条边长为0.4米,A的密度为2×103千克/米3,B质量为1千克.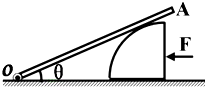 如图所示,横截面为四分之一圆(半径为R)的柱体放在水平地面上,一根匀质木棒OA长为3R,重为G.木棒的O端与地面上的铰链连接,木棒搁在柱体上,各处摩擦均不计.现用一水平推力F作用在柱体竖直面上,使柱体沿着水平地面向左缓慢移动.当木棒与地面的夹角θ=30°时,柱体对木棒的支持力为
如图所示,横截面为四分之一圆(半径为R)的柱体放在水平地面上,一根匀质木棒OA长为3R,重为G.木棒的O端与地面上的铰链连接,木棒搁在柱体上,各处摩擦均不计.现用一水平推力F作用在柱体竖直面上,使柱体沿着水平地面向左缓慢移动.当木棒与地面的夹角θ=30°时,柱体对木棒的支持力为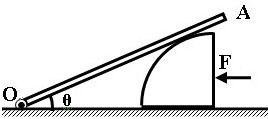 如图所示,横截面为四分之一圆(半径为R)的柱体放在水平地面上,一根匀质木棒OA长为3R,重为G.木棒的O端与地面上的铰链连接,木棒搁在柱体上,各处摩擦均不计.现用一水平推力F作用在柱体竖直面上,使柱体沿着水平地面向左缓慢移动.问:
如图所示,横截面为四分之一圆(半径为R)的柱体放在水平地面上,一根匀质木棒OA长为3R,重为G.木棒的O端与地面上的铰链连接,木棒搁在柱体上,各处摩擦均不计.现用一水平推力F作用在柱体竖直面上,使柱体沿着水平地面向左缓慢移动.问: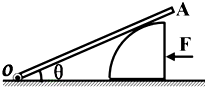 如图所示,横截面为四分之一圆(半径为R)的柱体放在水平地面上,一根匀质木棒OA长为3R,重为G.木棒的O端与地面上的铰链连接,木棒搁在柱体上,各处摩擦均不计.现用一水平推力F作用在柱体竖直面上,使柱体沿着水平地面向左缓慢移动.当木棒与地面的夹角θ=30°时,柱体对木棒的支持力为________.
如图所示,横截面为四分之一圆(半径为R)的柱体放在水平地面上,一根匀质木棒OA长为3R,重为G.木棒的O端与地面上的铰链连接,木棒搁在柱体上,各处摩擦均不计.现用一水平推力F作用在柱体竖直面上,使柱体沿着水平地面向左缓慢移动.当木棒与地面的夹角θ=30°时,柱体对木棒的支持力为________.