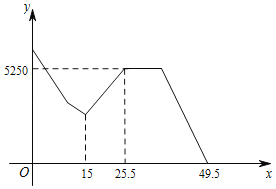
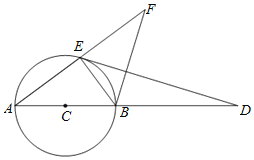
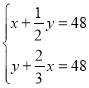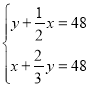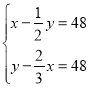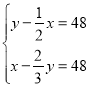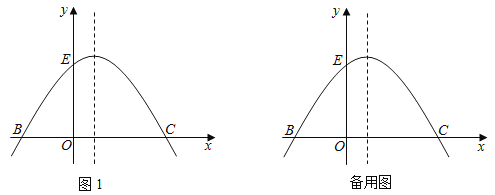【题目】已知函数
，
，探究函数图象和性质过程如下：
（1）下表是y与x的几组值，则解析式中的m＝ ，表格中的n＝ ;
x | ﹣5 | ﹣4 | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | … |
y |
|
|
| 1 |
| 3 |
| 4 |
| 3 | n | 0 | … |
（2）在平面直角坐标系中描出表格中各点，并画出函数图象：
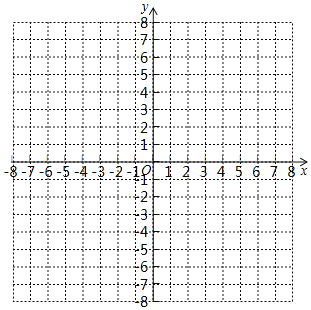
（3）若A（x1，y1）、B（x2，y2）、C（x3，y3）为函数图象上的三个点，其中x2+x3＞4且﹣1＜x1＜0＜x2＜2＜x3＜4，则y1、y2、y3之间的大小关系是 ；
（4）若直线y＝k+1与该函数图象有且仅有一个交点，则k的取值范围为 ．
【题目】在新的教学改革的推动下，某中学初年级积极推进英语小班教学．为了了解一段时间以来的英语小班教学的学习效果，年级组织了多次定时测试，现随机选取甲，乙两个班，从中各抽取20名同学在某一次定时测试中的英语成绩，过程如下，请补充完整
收集数据：
甲班的20名同学的英语成绩统计（单位：分）
86 90 60 76 92 83 56 76 85 70
96 96 90 68 78 80 68 96 85 81
乙班的20名同学的英语成绩统计（满分为100分）（单位：分）
78 96 75 76 82 87 60 54 87 72
100 82 78 86 70 92 76 80 98 78
整理数据：（成绩得分用x表示）
数量分数/ 班级 | 0≤x＜60 | 60≤x＜70 | 70≤x＜80 | 80≤x＜90 | 90≤x≤100 |
甲班（人数） | 1 | 3 | 4 | 6 | 6 |
乙班（人数） | 1 | 1 | 8 | 6 | 4 |
分析数据：
请回答下列问题：
（1）完成下表：
平均分 | 中位数 | 众数 | |
甲班 | 80.6 | 83 | a＝ |
乙班 | 80.35 | b＝ | 78 |
甲班成绩得分扇形图（x表示分数）
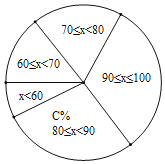
（2）在班成绩行分的扇形图中，成绩在70≤x＜80的扇形中，所对的圆心角α的度数 ，c＝ ．
（3）根据以上数据，你认为 班（填“甲”或“乙”）的同学的学习效果更好一些，你的理由是： ；
（4）若英语定时成绩不低于80分为优秀，请估计全年级1600人中优秀人数为多少？
