题目内容
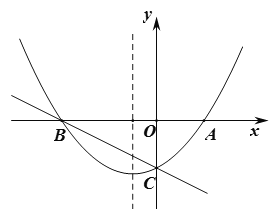
【题目】函数上的定点是指，一个含参数的函数无论参数取何值，函数的图象都过某一个点，这个点称为定点．例如，在函数y＝kx中，当x＝0时，无论参数k取何值，函数值y＝0，所以这个函数过定点（0，0）．
（1）分别求函数y＝kx+2k和y＝kx2﹣kx+2019的定点；
（2）若过原点的两条直线OA、OB分别与二次函数y＝
x2交于点A（m，m2）和点B（n，n2）（mn＜0）且OA⊥OB，试求直线AB上的定点；
（3）若直线CD：y＝kx+2k+5与抛物线y＝x2交于C、D两点，试在抛物线y＝x2上找一定点E，使∠CED＝90°，求点E的坐标，并求出点E到直线CD的最大距离．
【答案】（1）定点（﹣2，0）；定点（1，2019）、（0，2019）；（2）定点为E（2，4）；
【解析】
（1）y＝kx+2k＝k（x+2），当x＝﹣2时，y＝0，故过定点（﹣2，0），即可求解；
（2）直线AB的表达式为： 
，则tan∠AOM＝tan∠OBM，即： 
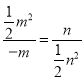，解得
，故直线AB的表达式为： 
，当x＝0时，y＝﹣2，故直线AB过点（0，﹣2）；
（3）直线CD的表达为：y＝（m+n）x﹣mn，则m+n＝k，mn＝﹣2k﹣5，tan∠CEM＝tan∠EDN，即：t2+（m+n）t+mn＝﹣1，即：t2﹣4+（t﹣2）k＝0，即可求解．
解：（1）y＝kx+2k＝k（x+2），当x＝﹣2时，y＝0，故过定点（﹣2，0）；
y＝kx2﹣kx+2019＝
，当x＝0或1时，y＝2019，故过定点（1，2019）、（0，2019）；
（2）将点A、B的坐标代入一次函数表达式：y＝kx+b并解得：
直线AB的表达式为： 
分别过点A、B作x轴的垂线于点M、N，则∠AOM＝∠OBN，
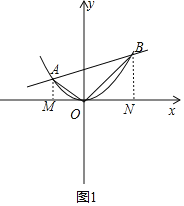
则tan∠AOM＝tan∠OBN，即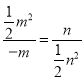： ，解得：
故直线AB的表达式为： 
，当x＝0时，y＝2，
故直线AB过点（0，2）；
（3）设点C、D的坐标分别为：（m，m2）、（n，n2），
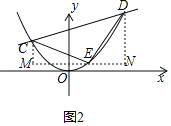
同理可得：直线CD的表达为：
则m+n＝k，mn＝﹣2k﹣5，
设点E（t，t2），
同理可得：tan∠CEM＝tan∠EDN，即：
化简得：t2+（m+n）t+mn＝﹣1，
即：t2﹣4+（t﹣2）k＝0，
当t＝2时，上式横成立，
故定点为E（2，4）；
直线CD：y＝kx+2k+5过定点H（﹣2，5），
∵点到直线的距离≤EH，
故点E到直线的最大距离为
【题目】在新的教学改革的推动下，某中学初年级积极推进英语小班教学．为了了解一段时间以来的英语小班教学的学习效果，年级组织了多次定时测试，现随机选取甲，乙两个班，从中各抽取20名同学在某一次定时测试中的英语成绩，过程如下，请补充完整
收集数据：
甲班的20名同学的英语成绩统计（单位：分）
86 90 60 76 92 83 56 76 85 70
96 96 90 68 78 80 68 96 85 81
乙班的20名同学的英语成绩统计（满分为100分）（单位：分）
78 96 75 76 82 87 60 54 87 72
100 82 78 86 70 92 76 80 98 78
整理数据：（成绩得分用x表示）
数量分数/ 班级 | 0≤x＜60 | 60≤x＜70 | 70≤x＜80 | 80≤x＜90 | 90≤x≤100 |
甲班（人数） | 1 | 3 | 4 | 6 | 6 |
乙班（人数） | 1 | 1 | 8 | 6 | 4 |
分析数据：
请回答下列问题：
（1）完成下表：
平均分 | 中位数 | 众数 | |
甲班 | 80.6 | 83 | a＝ |
乙班 | 80.35 | b＝ | 78 |
甲班成绩得分扇形图（x表示分数）
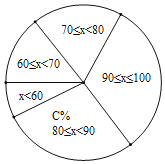
（2）在班成绩行分的扇形图中，成绩在70≤x＜80的扇形中，所对的圆心角α的度数 ，c＝ ．
（3）根据以上数据，你认为 班（填“甲”或“乙”）的同学的学习效果更好一些，你的理由是： ；
（4）若英语定时成绩不低于80分为优秀，请估计全年级1600人中优秀人数为多少？
【题目】某中学为了解七年级400名学生读书情况，随机调查了七年级50名学生读书的册数．统计数据如下表所示：
册数 | 0 | 1 | 2 | 3 | 4 |
人数 | 3 | 13 | 16 | 17 | 1 |
（1）求这50个样本数据的平均救，众数和中位数；
（2）根据样本数据，估计该校七年级400名学生在本次活动中读书多于3册的人数．
