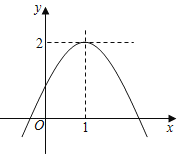题目内容
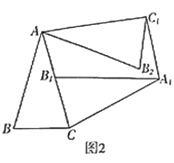
【题目】如图1,已知抛物线;C1:y=﹣![]() (x+2)(x﹣m)(m>0)与x轴交于点B、C(点B在点C的左侧),与y轴交于点E.
(x+2)(x﹣m)(m>0)与x轴交于点B、C(点B在点C的左侧),与y轴交于点E.
(1)求点B、点C的坐标;
(2)当△BCE的面积为6时,若点G的坐标为(0,b),在抛物线C1的对称轴上是否存在点H,使得△BGH的周长最小,若存在,则求点H的坐标(用含b的式子表示);若不存在,则请说明理由;
(3)在第四象限内,抛物线C1上是否存在点F,使得以点B、C、F为顶点的三角形与△BCE相似?若存在,求m的值;若不存在,请说明理由.
【答案】(1)点B、C的坐标分别为:(﹣2,0)、(m,0);(2)存在,点H(1,![]() b);(3)存在,m=2
b);(3)存在,m=2![]()
【解析】
(1)![]() ,令y=0,则x=﹣2或m,即可求解;
,令y=0,则x=﹣2或m,即可求解;
(2)点B关于函数对称轴的对称点为点C(m,0),连接CE交对称轴于点H,则点H为所求,即可求解;
(3)分△BEC∽△BCF、△BEC∽△FCB两种情况,分别求解即可.
解:(1)![]() ,令y=0,则x=﹣2或m,
,令y=0,则x=﹣2或m,
故点B、C的坐标分别为:(﹣2,0)、(m,0);
(2)存在,理由:
![]() ,令x=0,则y=2,故点E(0,2),
,令x=0,则y=2,故点E(0,2),
△BCE的面积为:![]() ,解得:m=4,
,解得:m=4,
则抛物线的对称轴为: ![]() ,
,
点B关于函数对称轴的对称点为点C(m,0),连接CE交对称轴于点H,则点H为所求,
将点C、E的坐标代入一次函数表达式并解得:
直线CE的表达式为: ![]() ,当x=1时,
,当x=1时,![]() ,
,
故点H(1,![]() b);
b);
(3)∵OE=OB=2,故∠EBO=45°,

过点F作FT⊥x轴于点F;
①当△BEC∽△BCF时,
则BC2=BEBF,∠FBO=EBO=45°,
则直线BF的函数表达式为:y=﹣x﹣2,故点F(x,﹣x﹣2);
将点F的坐标代入抛物线表达式得: ![]()
解得:x=﹣2(舍去)或2m,
故点F(2m,﹣2m﹣2),
则![]()
∵BC2=BEBF,
则![]() 解得:
解得: ![]() (舍去负值),
(舍去负值),
故![]()
②当△BEC∽△FCB时,
则BC2=BFEC,∠CBF=∠ECO,
则△BFT∽△COE,
则![]() ,则点
,则点![]()
将点F的坐标代入抛物线表达式得: ![]()
解得:x=﹣2(舍去)或m+2;
则点![]()
BC2=BFEC,则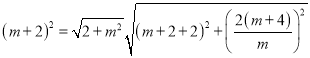
化简得:m3+4m2+4m=m3+4m2+4m+16,
此方程无解;
综上,m=2![]() .
.

 新思维寒假作业系列答案
新思维寒假作业系列答案【题目】已知函数![]() ,
,![]() ,探究函数图象和性质过程如下:
,探究函数图象和性质过程如下:
(1)下表是y与x的几组值,则解析式中的m= ,表格中的n= ;
x | ﹣5 | ﹣4 | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | … |
y |
|
|
| 1 |
| 3 |
| 4 |
| 3 | n | 0 | … |
(2)在平面直角坐标系中描出表格中各点,并画出函数图象:
(3)若A(x1,y1)、B(x2,y2)、C(x3,y3)为函数图象上的三个点,其中x2+x3>4且﹣1<x1<0<x2<2<x3<4,则y1、y2、y3之间的大小关系是 ;
(4)若直线y=k+1与该函数图象有且仅有一个交点,则k的取值范围为 .