【题目】对于平面直角坐标系xOy中的点P和⊙C，给出如下定义：若⊙C上存在两个点A、B，使得点P在射线BC上，且∠APB∠ACB（0°＜∠ACB＜180°），则称P为⊙C的依附点．

（1）当⊙O的半径为1时，

①已知点D（﹣1，0），E（0，﹣2），F（2.5，0），在点D、E、F中，⊙O的依附点是　 ；

②点T在直线y＝﹣x上，若T为⊙O的依附点，求点T的横坐标t的取值范围；

（2）⊙C的圆心在x轴上，半径为2，直线y＝﹣x+2与x轴、y轴分别交于点M、N，若线段MN上的所有点都是⊙C的依附点，直接写出圆心C的横坐标m的取值范围．

（1）依据题意，补全图形；

（2）求证：∠DAG＝∠MAB；

（3）用等式表示线段BM、DF与AD的数量关系，并证明．

（1）求点B的坐标；

（2）求抛物线C1的对称轴；

（3）把抛物线C1沿x轴翻折，得到一条新抛物线C2，抛物线C2与抛物线C1组成的图象记为G，若图象G与线段AB恰有一个交点时，结合图象，求a的取值范围．

收集数据：从A、B两个校区各随机抽取20名学生，进行了数学学业水平测试，测试成绩（百分制）如下：

A校区　　86　　74　　78　　81　　76　　75　　86　　70　　75　　90

　　　　　75　　79　　81　　70　　74　　80　　87　　69　　83　　77

B校区　　80　　73　　70　　82　　71　　82　　83　　93　　77　　80

　　　　　81　　93　　81　　73　　88　　79　　81　　70　　40　　83

整理、描述数据　按如下分数段整理、描述这两组样本数据：

（说明：成绩80分及以上的学业水平优秀，70﹣79分为淡定业水平良好，60﹣69分为学业水平合格，60分以下为学业水平不合格）

分析数据　两组样本数据的平均数、中位数、众数如下表所示：

其中m＝　 　；

得出结论：a．估计B校区九年级数学学业水平在优秀以上的学生人数为　　；

b．可以推断出　　校区的九年级学生的数学学业水平较高，理由为　 　（至少从两个不同的角度说明推断的合理性）．

【题目】如图1，M是圆中上一定点，P是弦AB上一动点，过点A作射线MP的垂线交圆于点C，连接PC．已知AB＝5cm，设A、P两点间的距离为xcm，A、C两点间的距离为y1cm，P、C两点的距离为y2cm．小帅根据学习函数的经验，分别对函数y1、y2随自变量x的变化而变化的规律进行了探究．

下面是小帅的探究过程，请补充完整：

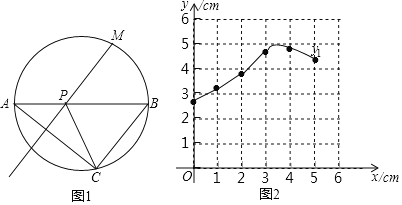
（1）按照表中自变量x的值进行取点，画图、测量，分别得到了y1、y2与x的几组对应值；

（2）在同一平面直角坐标系xOy中，描出补全后的表中各组数值所对应的点（x，y1），（x，y2），并画出函数y1、y2的图象；

（3）结合函数图象，解决问题：在点P的运动过程中，当AC与PC的差为最大值时，AP的长度约为　 　cm．

【题目】在平面直角坐标系xOy中，直线l：y＝kx+b（k≠0）与反比例函数y的图象的一个交点为M（1，m）．

（1）求m的值；

（2）直线l与x轴交于点A，与y轴交于点B，连接OM，设△AOB的面积为S1，△MOB的面积为S2，若S1≥3S2，求k的取值范围．

（1）求证：BD平分∠ABC；

（2）如果AB＝6，sin∠CBD，求PD的长．

（1）求证：四边形ABED为菱形；

（2）若BD＝6，∠E＝60°，求四边形ABEF的面积．

已知：直线l．

求作：△ABC，使得∠ACB＝90°，∠ABC＝30°．

作法：如图，

①在直线l上任取两点O，A；

②以点O为圆心，OA长为半径画弧，交直线l于点B；

③以点A为圆心，AO长为半径画弧，交于点C；

④连接AC，BC．

所以△ABC就是所求作的三角形．

根据小明设计的尺规作图过程：

（1）使用直尺和圆规，补全图形；（保留作图痕迹）

（2）完成下面的证明．

证明：在⊙O中，AB为直径，

∴∠ACB＝90°（① 　），（填推理的依据）

连接OC

∵OA＝OC＝AC，

∴∠CAB＝60°，

∴∠ABC＝30°（②　 　），（填推理的依据）

在这10名学生中，同时进入两项决赛的只有6人，进入立定跳远决赛的有8人，如果知道在同时进入两项决赛的6人中有“3508号”学生，没有“3307号”学生，那么的值是__________．