题目内容
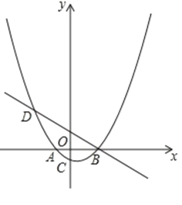
【题目】如图，已知抛物线y＝a（x+2）（x﹣4）（a为常数，且a＞0）与x轴从左至右依次交于A，B两点，与y轴交于点C，经过点B的直线y＝﹣
x+
抛物线的另一交点为D，且点D的横坐标为﹣5．
（1）求抛物线的函数表达式；
（2）该二次函数图象上有一点P（x，y）使得S△BCD＝S△ABP，求点P的坐标；
（3）设F为线段BD上一点（不含端点），连接AF，求2AF+DF的最小值．
【答案】（1）y＝
x2﹣
x﹣
；（2）(
，
)或(
，)；（3）
【解析】
（1）求出点D的坐标，利用待定系数法求出a的值即可．
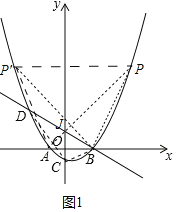
（2）如图1中，设直线BD交y轴于J，则J（0，
）．连接CD，BC．由S△PAB＝10
，推出
×6×|yP|＝10，推出yP＝
，再利用待定系数法构建方程求出点P的坐标即可．
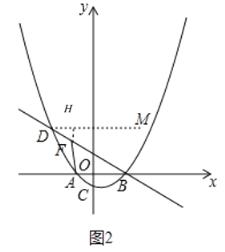
（3）如图2中，过点D作DM平行于x轴，首先证明∠BDM＝∠DBA＝30°，过F作FJ⊥DM于J，则有sin30°＝
，推出HF＝
，推出2AF+DF＝2（AF+
）＝2（AF+HF），当A、F、H三点共线时，即AH⊥DM时，2AF+DF＝2（AF+HF）取最小值．
解：（1）抛物线y＝a（x+2）（x﹣4），令y＝0，解得x＝﹣2或x＝4，
∴A（﹣2，0），B（4，0）．
∵直线y＝
，
当x＝﹣5时，y＝
∴D（﹣5，），
∵点D（﹣5，3）在抛物线y＝a（x+2）（x﹣4）上，
∴a（﹣5+2）（﹣5﹣4）＝，
∴a＝．
∴抛物线的函数表达式为：y＝
．
（2）如图1中，设直线BD交y轴于J，则J（0，）．连接CD，BC．
∵S△BDC＝
∴S△PAB＝
，
∴×6×|yP|＝
yP＝，
当y＝
时， 
，
解得x＝
，
∴P
或
，
当
方程无解，
∴满足条件的点P的坐标为或．
（3）如图2中，过点D作DM平行于x轴，作FH⊥DM于H，
∵D
，B（4，0），
∴tan∠DBA＝
，
∴∠DBA＝30°
∴∠BDM＝∠DBA＝30°，过F作FJ⊥DM于J，
则有sin30°＝，
∴
，
∴2AF+DF＝2（AF+）＝2（AF+HF），当A、F、H三点共线时，
即AH⊥DM时，2AF+DF＝2（AF+HF）取最小值
．
