Question

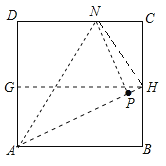
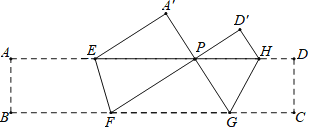
【题目】如图，已知点E，H在矩形ABCD的AD边上，点F，G在BC边上，将矩形ABCD沿EF，GH折叠，使点B和点C落在AD边上同一点P处．折叠后，点A的对应点为点A'，点D的对应点为点D'，若∠FPG＝90°，A'E＝3，D'H＝1，则矩形ABCD的周长等于_____．

Answer 1

【答案】12+6

【解析】

设AB＝CD＝x，由翻折可知：PA′＝AB＝x，PD′＝CD＝x，由锐角三角函数可求x，由勾股定理可求PE，PH的长，即可求解．

解：∵四边形ABC是矩形，

∴AB＝CD，AD＝BC，设AB＝CD＝x，

由翻折可知：PA′＝AB＝x，PD′＝CD＝x，∠C＝∠D'PG＝90°，∠B＝∠A'PF＝90°，

∵∠FPG＝90°，

∴∠FPG+∠A'PF＝180°，∠FPG+∠D'PG＝180°，

∴点A'，点P，点G共线，点D'，点P，点F共线，

∵A'E∥PF，

∴∠A'EP＝∠D'PH，

∴tan∠A'EP＝tan∠D'PH，

∴=.

∴x＝，

∴PA′＝AB＝＝PD′＝CD，

∴EP＝＝，

PH＝＝2，

∴AD＝2+6，

∴矩形ABCD的周长等于＝2×（+2+6）＝12+6，

故答案为：12+6．