题目内容
一个n边形中，除了一个内角外，其余内角和是1020°，那么这个未知角是 度，这个多形是 边形．
考点：多边形内角与外角
专题：计算题
分析：n边形的内角和为（n-2）×180°，即多边形的内角和为180°的整数倍，用1020°除以180°，所得余数和去掉的一个内角互补．
解答：解：∵1020°÷180°=5…120°，
∴去掉的内角为180°-120°=60°，
设这个多边形为n边形，
则（n-2）×180°=1020°+60°，
解得n=8，
故答案为：60°，八．
∴去掉的内角为180°-120°=60°，
设这个多边形为n边形，
则（n-2）×180°=1020°+60°，
解得n=8，
故答案为：60°，八．
点评：本题考查了多边形内角与外角．关键是利用多边形的内角和为180°的整数倍，求多边形去掉的一个内角度数．
练习册系列答案
培优好卷单元加期末卷系列答案
相关题目
如图，在△ABC中，cosB=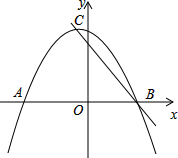
已知二次函数y=ax2+bx+c（a≠0）的图象与x轴交于点A（-2，0）、B（x1，0），且1＜x1＜2，与y轴正半轴的交点在（0，2）的上方，顶点为C．直线y=kx+m（k≠0）经过点C、B．则下列结论：