题目内容
某射击运动员在一次比赛中(共10次射击,每次射击最多是10环),前6次射击共中52环,如果他要打破89环的记录,则第七次射击不能少于( )环.
| A、5 | B、6 | C、7 | D、8 |
考点:一元一次不等式的应用
专题:计算题
分析:根据题中的信息,要打破89环,则最少需要90环,设第7次成绩为x环,第8,9,10次的成绩都为10环,则可以列出不等式,从而得出答案.
解答:解:设他第7次射击的成绩为x环,得:
52+x+30>89
解得x>7.
由于x是正整数且大于7,得:x≥8.
答:运动员第7次射击不能少于8环,
故选:D.
52+x+30>89
解得x>7.
由于x是正整数且大于7,得:x≥8.
答:运动员第7次射击不能少于8环,
故选:D.
点评:此题主要考查了一元一次不等式的应用,解决问题的关键是读懂题意,依题意列出不等式进行求解.

练习册系列答案
相关题目
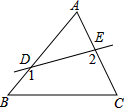 如图,△ABC中,∠A=60°,则∠1+∠2的度数为( )
如图,△ABC中,∠A=60°,则∠1+∠2的度数为( )| A、120° | B、180° |
| C、240° | D、300° |
 如图,已知CE是△ABC的中线,DE⊥AB交外角∠BCF的平分线于D,∠ACB=60°,证明:BC=AC+CD.
如图,已知CE是△ABC的中线,DE⊥AB交外角∠BCF的平分线于D,∠ACB=60°,证明:BC=AC+CD.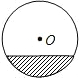 一根水平放置的圆柱形输水管道横截面如图所示,其中有水部分水面宽8m,最深处水深2m,则此输水管道的直径是多少?
一根水平放置的圆柱形输水管道横截面如图所示,其中有水部分水面宽8m,最深处水深2m,则此输水管道的直径是多少?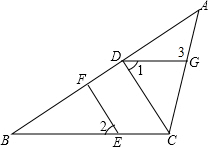 如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F.
如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F.