题目内容
已知Rt△ABC的斜边AB=8,AC=4,以点C为圆心作圆,当半径R等于 时,AB与⊙O相切.
考点:切线的判定
专题:计算题
分析:首先根据题意画出图形,再过点C作CD⊥AB于点D,由Rt△ABC的斜边AB=8,AC=4,可求得BC的长,然后由三角形面积可得CD=
=2
,即可求得答案.
| AC•BC |
| AB |
| 3 |
解答: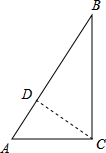 解:过点C作CD⊥AB于点D,
解:过点C作CD⊥AB于点D,
∵Rt△ABC的斜边AB=8,AC=4,
∴CB=
=4
,
∵S△ABC=
AC•BC=
AB•CD,
∴CD=
=2
,
∴当半径R等于2
时,AB与⊙O相切.
故答案为:2
.
 解:过点C作CD⊥AB于点D,
解:过点C作CD⊥AB于点D,∵Rt△ABC的斜边AB=8,AC=4,
∴CB=
| AB2-AC2 |
| 3 |
∵S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
∴CD=
| AC•BC |
| AB |
| 3 |
∴当半径R等于2
| 3 |
故答案为:2
| 3 |
点评:此题考查了切线的判定、勾股定理以及三角形面积问题.此题难度不大,注意掌握数形结合思想的应用.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
 如图,一艘货轮由港口A出发向正东方向行驶,在港口A处时,测得灯塔B在港口A的南偏东30°方向,小岛C在港口A的南偏东60°方向,当这艘货轮行驶60海里到点D处时,小岛C恰好在点D处的正南方向,此时测得灯塔B在南偏西60°的方向,求:
如图,一艘货轮由港口A出发向正东方向行驶,在港口A处时,测得灯塔B在港口A的南偏东30°方向,小岛C在港口A的南偏东60°方向,当这艘货轮行驶60海里到点D处时,小岛C恰好在点D处的正南方向,此时测得灯塔B在南偏西60°的方向,求: 如图,已知CE是△ABC的中线,DE⊥AB交外角∠BCF的平分线于D,∠ACB=60°,证明:BC=AC+CD.
如图,已知CE是△ABC的中线,DE⊥AB交外角∠BCF的平分线于D,∠ACB=60°,证明:BC=AC+CD.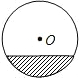 一根水平放置的圆柱形输水管道横截面如图所示,其中有水部分水面宽8m,最深处水深2m,则此输水管道的直径是多少?
一根水平放置的圆柱形输水管道横截面如图所示,其中有水部分水面宽8m,最深处水深2m,则此输水管道的直径是多少?