题目内容
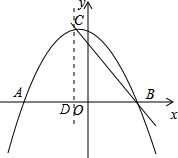
 已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(-2,0)、B(x1,0),且1<x1<2,与y轴正半轴的交点在(0,2)的上方,顶点为C.直线y=kx+m(k≠0)经过点C、B.则下列结论:
已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(-2,0)、B(x1,0),且1<x1<2,与y轴正半轴的交点在(0,2)的上方,顶点为C.直线y=kx+m(k≠0)经过点C、B.则下列结论:①b>a;②2a-b>-1;③2a+c<0;④k>a+b;⑤k<-1,
其中正确的结论有
考点:二次函数图象与系数的关系
专题:计算题
分析:首先根据抛物线的开口方向向下可得到a<0,抛物线交y轴于正半轴,则c>0,而抛物线与x轴的交点中,1<x1<2,x2=-2,说明抛物线的对称轴在-1~0之间,即x=-
>-1,可根据这些条件以及函数图象上一些特殊点的坐标来进行判断,即可得到正确的选项.
| b |
| 2a |
解答:解:①由图知:抛物线的开口向下,则a<0.
对称轴在x轴的左侧,因此,a、b同号,则b<0
∵-2+x1=-
,1<x1<2,
∴0<
<1,
∴b>a.
故①正确;
②∵抛物线交x轴与点(-2,0)
∴4a-2b+c=0
∵c>2
∴4a-2b=-c<-2
即2a-b<-1.
故②错误;
③∵二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(-2,0),
∴4a-2b+c=0
∵b>a,
∴2b>2a,
∴4a-2b>2a,
∴4a-2b+c>2a+c,即0>2a+c,
∴2a+c<0,
故③正确;
⑤如图,过顶点C作CD⊥AB于点D.
则k=-
.
∵CD>2,BD=AD<1,
∴
>2,
∴k<-2,
故⑤错误;
④∵当x=1时,y>0,
∴a+b+c>0,
∵c>2,
∴a+b>-2.
又由⑤知,k<-2,
∴k<a+b.
故④错误;
综上所述,正确的结论有①③.
故答案是:①③.
对称轴在x轴的左侧,因此,a、b同号,则b<0
∵-2+x1=-
| b |
| a |
∴0<
| b |
| a |
∴b>a.
故①正确;
②∵抛物线交x轴与点(-2,0)
∴4a-2b+c=0
∵c>2
∴4a-2b=-c<-2
即2a-b<-1.
故②错误;

③∵二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(-2,0),
∴4a-2b+c=0
∵b>a,
∴2b>2a,
∴4a-2b>2a,
∴4a-2b+c>2a+c,即0>2a+c,
∴2a+c<0,
故③正确;
⑤如图,过顶点C作CD⊥AB于点D.
则k=-
| CD |
| BD |
∵CD>2,BD=AD<1,
∴
| CD |
| BD |
∴k<-2,
故⑤错误;
④∵当x=1时,y>0,
∴a+b+c>0,
∵c>2,
∴a+b>-2.
又由⑤知,k<-2,
∴k<a+b.
故④错误;
综上所述,正确的结论有①③.
故答案是:①③.
点评:本题主要考查对二次函数图象与系数的关系,抛物线与x轴的交点,二次函数图象上点的坐标特征等知识点的理解和掌握,能根据图象确定与系数有关的式子的正负是解此题的关键.

练习册系列答案
相关题目
 如图,四边形ABCD是正方形,点G是BC上任意一点,BE⊥AG于点E,点F为AE上一点,且AE-BE=EF,求证:BE∥DF.
如图,四边形ABCD是正方形,点G是BC上任意一点,BE⊥AG于点E,点F为AE上一点,且AE-BE=EF,求证:BE∥DF.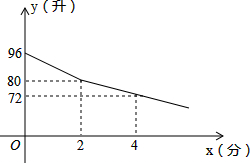 某校部分住校生,放学后到学校锅炉房打水,每人接水2升,他们先同时打开两个放水笼头,后来因故障关闭一个放水笼头.假设前后两人接水间隔时间忽略不计,且不发生泼洒,锅炉内的余水量y(升)与接水时间x(分)的函数图象如图.请结合图象,回答下列问题:
某校部分住校生,放学后到学校锅炉房打水,每人接水2升,他们先同时打开两个放水笼头,后来因故障关闭一个放水笼头.假设前后两人接水间隔时间忽略不计,且不发生泼洒,锅炉内的余水量y(升)与接水时间x(分)的函数图象如图.请结合图象,回答下列问题: 如图,已知CE是△ABC的中线,DE⊥AB交外角∠BCF的平分线于D,∠ACB=60°,证明:BC=AC+CD.
如图,已知CE是△ABC的中线,DE⊥AB交外角∠BCF的平分线于D,∠ACB=60°,证明:BC=AC+CD.