题目内容
【题目】某家禽养殖场,用总长为110m的围栏靠墙(墙长为22m)围成如图所示的三块矩形区域,矩形AEHG与矩形CDEF面积都等于矩形BFHG面积的一半,设AD长为xm,矩形区域ABCD的面积为ym2 . 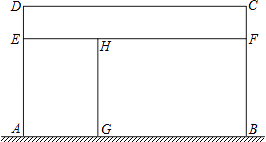
(1)求y与x之间的函数关系式,并写出自变量x的取值范围;
(2)当x为何值时,y有最大值?最大值是多少?
【答案】
(1)解:∵矩形AEHG与矩形CDEF面积都等于矩形BFHG面积的一半,
∴矩形AEFB面积是矩形CDEF面积的3倍,
∴AD=3DE,
∵AD=x,
∴GH= ![]() x,
x,
∵围栏总长为110m,
∴2x+ ![]() x+2CD=110,
x+2CD=110,
∴CD=55﹣ ![]() x,
x,
∴y=x(55﹣ ![]() x)=﹣
x)=﹣ ![]() x2+55x,
x2+55x,
∴自变量x的取值范围为:24≤x<40;
(2)解:∵y=﹣ ![]() x2+55x=﹣
x2+55x=﹣ ![]() ( x2﹣40 x)=﹣
( x2﹣40 x)=﹣ ![]() ( x﹣20)2+550,
( x﹣20)2+550,
∵自变量x的取值范围为:24≤x<40,且二次项系数为﹣ ![]() <0,
<0,
∴当x=24时,y有最大值,最大值为528平方米.
【解析】(1)由矩形AEHG与矩形CDEF面积都等于矩形BFHG面积的一半,得到矩形AEFB面积是矩形CDEF面积的3倍,根据矩形面积公式得到二次函数,求出自变量x的取值范围;(2)根据自变量x的取值范围,得到y的最大值.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目