Question

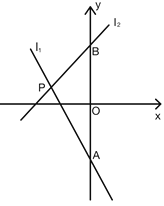
【题目】如图，在直角坐标系中，有菱形，点的坐标是，双曲线经过点，且，则的值为（ ）

A. 40 B. 48 C. 64 D. 80

Answer 1

【答案】B

【解析】

过C作CD垂直于x轴，交x轴于点D，由菱形的面积等于对角线乘积的一半，根据已知OB与AC的乘积求出菱形OABC的面积，而菱形的面积可以由OA乘以CD来求，根据OA的长求出CD的长，在中，利用勾股定理求出OD的长，确定出C的坐标，代入反比例解析式中即可求出k的值．

过C作CD垂直于x轴，交x轴于点D，

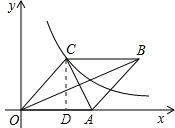
∵四边形OABC是菱形，OB与AC为两条对角线，且OBAC=160，

∴菱形OABC的面积为80，即OACD=80，

∵OA=AC=10，

∴CD=8，

在Rt△OCD中，

∵OC=10，CD=8，

∴

∴C(6,8)，

∴k=6×8=48.

故选：B.