题目内容
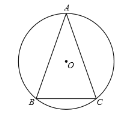
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,圆
,圆![]() 是
是![]() 的外接圆.
的外接圆.
(1)求圆![]() 的半径;
的半径;
(2)若在同一平面内的圆![]() 也经过
也经过![]() 、
、![]() 两点,且
两点,且![]() ,请直接写出圆
,请直接写出圆![]() 的半径的长.
的半径的长.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]()
【解析】
(1)过点![]() 作
作![]() ,垂足为
,垂足为![]() ,连接
,连接![]() ,根据垂直平分线的性质可得
,根据垂直平分线的性质可得![]() 在
在![]() 上,根据垂径定理即可求出BD,再根据勾股定理即可求出AD,设
上,根据垂径定理即可求出BD,再根据勾股定理即可求出AD,设![]() ,根据勾股定理列出方程即可求出半径;
,根据勾股定理列出方程即可求出半径;
(2)根据垂直平分线的判定可得点P在BC的中垂线上,即点P在直线AD上,然后根据点A和点P的相对位置分类讨论,然后根据勾股定理分别求出半径即可.
(1)过点![]() 作
作![]() ,垂足为
,垂足为![]() ,连接
,连接![]()

∵![]() ,
,![]()
∴![]() 垂直平分
垂直平分![]()
∵![]()
∴点![]() 在
在![]() 的垂直平分线上,即
的垂直平分线上,即![]() 在
在![]() 上.
上.
∵![]()
∴![]()
∵在![]() 中,
中,![]() ,
,![]()
∴![]()
设![]() ,则
,则![]()
∵在![]() 中,
中,![]() ,
,
∴![]() ,即
,即![]()
解得![]() ,即圆
,即圆![]() 的半径为
的半径为![]() .
.
(2)∵圆![]() 也经过
也经过![]() 、
、![]() 两点,
两点,
∴PA=PB
∴点P在BC的中垂线上,即点P在直线AD上
①当点P在A下方时,此时AP=2,如下图所示,连接PB

∴PD=AD-AP=4
根据勾股定理PB=![]() ;
;
②当点P在A上方时,此时AP=2,如下图所示,连接PB
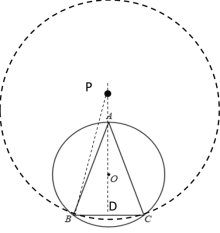
∴PD=AD+AP=8
根据勾股定理PB=![]() .
.
综上所述:圆![]() 的半径的长为
的半径的长为![]() 或
或![]() .
.

练习册系列答案
相关题目