题目内容
【题目】如图1、2是底面半径为1cm，母线长为2cm的圆柱体和圆锥体模型．现要用长为2πcm，宽为4cm的长方形彩纸（如图3）装饰圆柱、圆锥模型表面．已知一个圆柱和一个圆锥模型为一套，长方形彩纸共有122张，用这些纸最多能装饰多少套模型呢？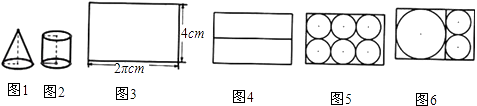 
老师：“长方形纸可以怎么裁剪呢？”
学生甲：“可按图4方式裁剪出2张长方形．”
学生乙：“可按图5方式裁剪出6个小圆．”
学生丙：“可按图6方式裁剪出1个大圆和2个小圆．”
老师：尽管还有其他裁剪方法，但为裁剪方便，我们就仅用这三位同学的裁剪方法！
（1）计算：圆柱的侧面积是cm2 ， 圆锥的侧面积是cm2 ．
（2）1张长方形彩纸剪拼后最多能装饰个圆锥模型；5张长方形彩纸剪拼后最多能装饰个圆柱体模型．
（3）求用122张彩纸对多能装饰的圆锥、圆柱模型套数．
【答案】
（1）4π；2π
（2）2；6
（3）解：设做x套模型，则每套模型中做圆锥的需要 
张纸，作圆柱需要 
张纸，
∴ + ≤122，
解得：x≤ 
，
∵x是6的倍数，取x=90，做90套模型后剩余长方形纸片的张数是
122﹣（45+75）=2张，
2张纸够用这三位同学的裁剪方法不能做一套模型．
∴最多能做90套模型．
【解析】解：（1）圆柱的地面底面周长是2π，则圆柱的侧面积是2π×2=4πcm2 ， 圆锥的侧面积是 
×2π×2=2πcm2；（2）圆柱的底面积是：πcm2 ， 则圆柱的表面积是：6πcm2 ， 圆锥的表面积是：3πcm2 ． 一张纸的面积是：4×2π=8π，
则1张长方形彩纸剪拼后最多能装饰 2个圆锥模型；5张长方形彩纸剪拼后最多能装饰6个圆柱体模型，
【考点精析】关于本题考查的圆锥的相关计算和圆柱的相关计算，需要了解圆锥侧面展开图是一个扇形，这个扇形的半径称为圆锥的母线；圆锥侧面积S=πrl；V圆锥=1/3πR2h.；圆柱的体积： V圆柱=πR2h才能得出正确答案．
