题目内容
【题目】己知二次函数
．
（1）将化成
的形式为________；
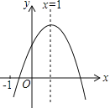
（2）此函数与
轴的交点坐标为________；
（3）在平面直角坐标系
中画出这个二次函数的图象(不用列表)；
（4）直接写出当
时，
的取值范围．
【答案】（1）
；（2）(-1，0)，(3，0)；（3）见解析；（4）-4＜y＜5
【解析】
（1）直接配方即可化为顶点式；
（2）把y=0代入，解方程即可；
（3）通过列表、描点、连线，作图即可；
（4）根据函数的图象求解即可．
（1）
故答案为：
（2）当y=0时，
解得：
∴与x轴的交点坐标为：(-1，0)，(3，0)
故答案为：(-1，0)，(3，0)
（3）列表：
x | … | -1 | 0 | 1 | 2 | 3 | … |
y=x2-2x-3 | … | 0 | -3 | -4 | -3 | 0 | … |
描点、连线．
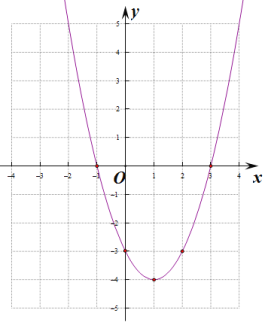
（4）根据图象可得：
当x=-2时，y=5；顶点坐标为（1，-4）
即函数的最小值为-4，
∴当
时，-4＜y＜5
练习册系列答案
相关题目
