题目内容
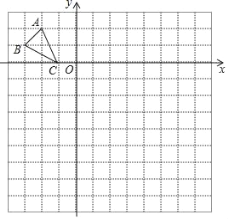
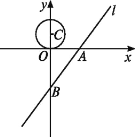
【题目】如图,已知直线l的解析式是y=![]() x-4,并且与x轴、y轴分别交于A,B两点.一个半径为1.5的☉C,圆心C从点(0,1.5)开始以每秒移动0.5个单位长度的速度沿着y轴向下运动,当☉C与直线l相切时,则该圆运动的时间为( )
x-4,并且与x轴、y轴分别交于A,B两点.一个半径为1.5的☉C,圆心C从点(0,1.5)开始以每秒移动0.5个单位长度的速度沿着y轴向下运动,当☉C与直线l相切时,则该圆运动的时间为( )
A. 3 s或6 sB. 6 s或10 sC. 3 s或16 sD. 6 s或16 s
【答案】D
【解析】
由直线l的解析式可确定A(3,0)和B(0,-4),由此可得AB=5以及sin∠ABC;由题可知,当☉C在直线l上方与直线l相切时,圆心到直线的距离为1.5,则由sin∠ABC即可求解此时BC的长度,进而求解运动时间;☉C在直线l下方与直线l相切时的求解方法同上.
解:如图,共有两种相切方式,

由直线l的解析式y=![]() x-4,可得A(3,0)和B(0,-4),则AB=5,sin∠ABC=
x-4,可得A(3,0)和B(0,-4),则AB=5,sin∠ABC=![]() ,
,
当☉C在直线l上方与直线l相切时,CD=1.5,则BC=CD÷sin∠ABC=1.5÷![]() =2.5,即C点的运动距离为1.5+4-2.5=3,则运动时间为3÷0.5=6s;
=2.5,即C点的运动距离为1.5+4-2.5=3,则运动时间为3÷0.5=6s;
当☉C在直线l下方与直线l相切时,CD=1.5,则BC=CD÷sin∠ABC=1.5÷![]() =2.5,即C点的运动距离为1.5+4+2.5=8,则运动时间为8÷0.5=16s;
=2.5,即C点的运动距离为1.5+4+2.5=8,则运动时间为8÷0.5=16s;
故选择D.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目