Question

【题目】已知四边形ABCD是平行四边形（如图），把△ABD沿对角线BD翻折180°得到△AˊBD.

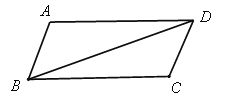
（1）利用尺规作出△AˊBD.（要求保留作图痕迹，不写作法）；

（2）设D Aˊ 与BC交于点E，求证：△BAˊE≌△DCE.

Answer 1

【答案】见解析

【解析】解：（1）作图如下：

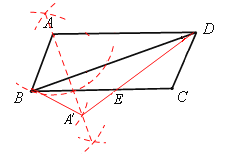
（2）证明：∵四边形ABCD是平行四边形，∴∠A=∠B，AB=DC。

∵△ABD沿对角线BD翻折180°得到△AˊBD，

∴∠Aˊ=∠A，AˊB= AB。∴∠Aˊ=∠B，AˊB= DC。

又∵∠AˊEB=∠DEC，∴△BAˊE≌△DCE（AAS）。

（1）作法：①过点A作BD的垂线；

②以点B 为圆心，AB为半径画弧，交BD的垂线于点Aˊ；

③连接AˊB，AˊD。

则△AˊBD即为所求。

（2）由平行四边形和翻折对称的性质，应用AAS即可证明。