题目内容
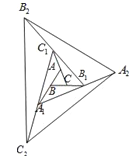
【题目】如图,△ABC的面积为1,分别倍长(延长一倍)AB,BC,CA得到△A1B1C1,再分别倍长A1B1,B1C1,C1A1得到△A2B2C2.…按此规律,倍长n次后得到的△A2017B2017C2017的面积为________.
【答案】![]() .
.
【解析】连接AB1、BC1、CA1,根据等底等高的三角形面积相等,
可知△A1BC、△A1B1C、△AB1C、△AB1C1、△ABC1、△A1BC1、△ABC的面积都相等,
所以△A1B1C1的面积S1=7S△ABC,
同理△A2B2C2的面积S2=7S1=72S△ABC,
依此类推△A2017B2017C2017的面积S2017=72017S△ABC,
∵△ABC的面积为1,
∴S2017=72017.
故答案为72017.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目