题目内容
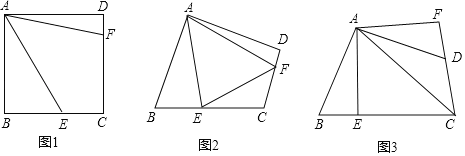
【题目】（1）如图1，点E、F分别在正方形ABCD的边BC、CD上，∠EAF=45°，求证：EF=BE+FD．
（2）如图2，四边形ABCD中，∠BAD≠90°，AB=AD，∠B+∠D=180°，点E、F分别在边BC、CD上，则当∠EAF与∠BAD满足什么关系时，仍有EF=BE+FD，说明理由．
（3）如图3，四边形ABCD中，∠BAD≠90°，AB=AD，AC平分∠BCD，AE⊥BC于E，AF⊥CD交CD延长线于F，若BC=8，CD=3，则CE= .（不需证明）
【答案】（1）详见解析；（2）∠BAD=2∠EAF，理由详见解析；（3）CE=5.5.
【解析】试题分析：（1）将△ABE绕点A旋转使得AB与AD重合，然后证明△AFG≌△AFE，再利用全等三角形对应的边相等的性质不难证明；（2）首先延长CB至M，使BM=DF，连接AM，构造△ABM≌△ADF，再证明△FAE≌△MAE，最后将相等的边进行转化整理即可证明.
试题解析：
（1）证明：把△ABE绕点A逆时针旋转90°至△ADG，如图1所示：
则△ADG≌△ABE，
∴AG=AE，∠DAG=∠BAE，DG=BE，
又∵∠EAF=45°，即∠DAF+∠BAE=∠EAF=45°，
∴∠GAF=∠FAE，
在△GAF和△FAE中， 
, ，
∴△AFG≌△AFE（SAS）．
∴GF=EF．
又∵DG=BE，
∴GF=BE+DF，
∴BE+DF=EF．
（2）∠BAD=2∠EAF．理由如下：
如图2所示，延长CB至M，使BM=DF，连接AM，
∵∠ABC+∠D=180°，∠ABC+∠ABM=180°，
∴∠D=∠ABM，
在△ABM和△ADF中， 
，
∴△ABM≌△ADF（SAS）
∴AF=AM，∠DAF=∠BAM，
∵∠BAD=2∠EAF，
∴∠DAF+∠BAE=∠EAF，
∴∠EAB+∠BAM=∠EAM=∠EAF，
在△FAE和△MAE中， 
，
∴△FAE≌△MAE（SAS），
∴EF=EM=BE+BM=BE+DF，
即EF=BE+DF．
（3）CE=5.5
