题目内容
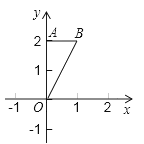
如图,在边长为9的正方形ABCD中, F为AB上一点,连接CF.过点F作FE⊥CF,交AD于点E，若AF＝3,则AE等于（ ） 
| A．1 | B．1．5 | C．2 | D．2．5 |
C．
解析试题分析：根据正方形性质得出AD=AB=BC=9，∠A=∠B=90°，求出∠AEF=∠CFB，证△AEF∽△BFC，得出比例式，即可求出答案：
∵四边形ABCD是正方形，∴AD=AB=BC=9，∠A=∠B=90°.
∵FE⊥CF，∴∠EFC=90°.∴∠AEF+∠EFA=90°，∠AFE+∠CFB=90°.∴∠AEF=∠CFB.
∴△AEF∽△BFC．∴
，即
，解得AE=2.
故选C．
考点：1.相似三角形的判定与性质；2.正方形的性质．
练习册系列答案
阅读快车系列答案
相关题目
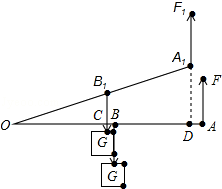
如图，一天晚上，小颖由路灯A下的B处走到C处时，测得影子CD的长为1米，当她继续往前走到D处时，测得此时影子DE的长刚好是自己的身高，已知小颖的身高为1.5米，那么路灯A的高度AB为（ ）
| A．3米 | B．4.5米 | C．6米 | D．8米 |
如图，△ABC为等腰直角三角形，∠BAC=90°，BC=2，E为AB上任意一动点，以CE为斜边作等腰Rt△CDE，连接AD，下列说法：
①∠BCE=∠ACD；②AC⊥ED；③△AED∽△ECB；④AD∥BC；⑤四边形ABCD的面积有最大值，且最大值为
．其中，正确的结论是 。
| A．①②④ | B．①③⑤ | C．②③④ | D．①④⑤ |
如图，在平行四边形ABCD中，AC与BD交于点O，E为OD的中点，连接AE并延长交DC于点F，则DF∶FC=
| A．1∶4 | B．1∶3 | C．2∶3 | D．1∶2 |
若△ABC∽△A′B′C′，∠A=40°，∠B=60°，则∠C′等于 （ ）
| A．20°； | B．40°； | C．60°； | D．80°． |
的直角边
在
轴上，点
在第一象限内，
，
，若将△
按顺时针方向旋转90°，则点