题目内容
如图，A，B两地被池塘隔开，小明通过下列方法测出了A、B间的距离：先在AB外选一点C，然后测出AC，BC的中点M，N，并测量出MN的长为12m，由此他就知道了A、B间的距离．有关他这次探究活动的描述错误的是（ ）
A. AB=24m B. MN∥AB
C. △CMN∽△CAB D. CM：MA=1：2
D．
解析试题分析：根据三角形的中位线和相似三角形的判定与性质逐一作出判定：
∵M、N分别是AC，BC的中点，∴MN∥AB，MN=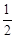
AB. 故选项B正确.
∵MN=12m，∴AB="2MN=2×12=24m." 故选项A正确.
∵MN∥AB，∴△CMN∽△CAB. 故选项C正确.
∵M是AC的中点，∴CM="MA." ∴CM：MA=1：1. 故选项D错误.
故选D．
考点：1.三角形中位线定理；2.相似三角形的应用．
习题精选系列答案
如图,在边长为9的正方形ABCD中, F为AB上一点,连接CF.过点F作FE⊥CF,交AD于点E，若AF＝3,则AE等于（ ） 
| A．1 | B．1．5 | C．2 | D．2．5 |
如图是小明设计用手电来测量某古城墙高度的示意图,点P处放一水平的平面镜,光线从点A出发经平面镜反射后刚好射到古城墙CD的顶端C处，已知AB⊥BD，CD⊥BD，且测得AB=1.2米，BP=1.8米，PD=12米， 那么该古城墙的高度是（ ）
| A．6米 | B．8米 | C．18米 | D．24米 |
如图,在△
中,点
分别在
边上,
∥
,若
,
,则
等于
A． | B． | C． | D． |
设边长为2a的正方形的中心A在直线l上，它的一组对边垂直于直线l，半径为r的⊙O的圆心O在直线l上运动，点A、O间距离为d．
（1）如图①，当r＜a时，根据d与a、r之间关系，将⊙O与正方形的公共点个数填入下
表：(6分)
| d、a、r之间关系 | 公共点的个数 |
| d＞a＋r | |
| d＝a＋r | |
| a－r＜d＜a＋r | |
| d＝a－r | |
| d＜a－r | |
当r＜a时，⊙O与正方形的公共点的个数可能有 个；
（2）如图②，当r＝a时，根据d与a、r之间关系，将⊙O与正方形的公共点个数填入下表：(5分)
| d、a、r之间关系 | 公共点的个数 |
| d＞a＋r | |
| d＝a＋r | |
| a≤d＜a＋r | |
| d＜a | |
所以，当r＝a时，⊙O与正方形的公共点个数可能有 个；
（3）如图③，当⊙O与正方形有5个公共点时，试说明r＝
a；(5分)
如图，在平面直角坐标系中，以原点O为位似中心，将△ABO扩大到原来的2倍，得到△A′B′O.若点A的坐标是(1，2)，则点A′的坐标是( )
| A．(2，4) | B．(－1，－2) |
| C．(－2，－4) | D．(－2，－1) |