题目内容
已知正六边形的半径为20cm，则它的外接圆与内切圆组成的圆环的面积是分析：经过圆心O作圆的内接正n边形的一边AB的垂线OC，垂足是C．连接OA，则在直角△OAC中，∠O=
．OC是边心距r，OA即半径R．AB=2AC=a，根据三角函数即可求解．
| 180° |
| n |
解答：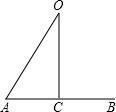
解：正六边形的半径为20cm，
则它的外接圆的半径也是20cm，
它的内切圆的半径=20×
=10
cm，
所以圆环的面积=π[202-（10
）2]=100πcm2．
解：正六边形的半径为20cm，则它的外接圆的半径也是20cm，
它的内切圆的半径=20×
| ||
| 2 |
| 3 |
所以圆环的面积=π[202-（10
| 3 |
点评：本题利用了正六边形的边长与它的外接圆的半径的关系和与内切圆的半径的关系及圆的面积公式求解．
练习册系列答案
相关题目
已知正六边形的半径为2，那么这个正六边形的边长为（ ）
| A、2 | ||
B、
| ||
C、
| ||
| D、1 |
已知正六边形的半径为2，则这个正六边形的面积是（ ）
| A、6 | ||
| B、12 | ||
C、6
| ||
D、12
|