Question

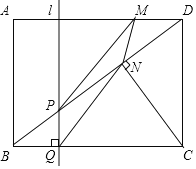
【题目】在平面直角坐标系xOy中有不重合的两个点Q（x1，y1）与P（x2，y2），若Q、P为某个直角三角形的两个锐角顶点，且该直角三角形的直角边均与x轴或y轴平行（或重合），则我们将该直角三角形的两条直角边的边长之和称为点Q与点P之间的“直距”，记作DPQ，特别地，当PQ与某条坐标轴平行（或重合）时，线段PQ的长即为点Q与点P之间的“直距”，例如在图1中，点P（1，1），点Q（3，2），此时点Q与点P之间的“直距”DPQ＝3．

（1）①已知O为坐标原点，点A（2，－1），B（－2，0），则DAO＝________，DBO＝________．

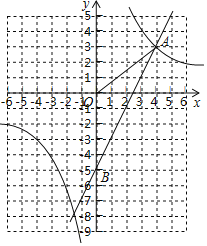
②点C在直线y＝－x＋3上，请你求出DCO的最小值．

（2）点E是以原点O为圆心，1为半径的圆上的一个动点，点F是直线y＝2x＋4上一动点，请你直接写出点E与点F之间“直距”DEF的最小值．

Answer 1

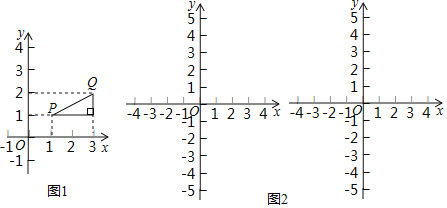
【答案】（1）①3，2；②最小值为3；（2）

【解析】

（1）①根据点Q与点P之间的“直距”的定义计算即可；

②如图3中，由题意，当DCO为定值时，点C的轨迹是以点O为中心的正方形（如左边图），当DCO＝3时，该正方形的一边与直线y＝－x＋3重合（如右边图），此时DCO定值最小，最小值为3；

（2）如图4中，平移直线y＝2x＋4，当平移后的直线与⊙O在左边相切时，设切点为E，作EF∥x轴交直线y＝2x＋4于F，此时DEF定值最小；

解：（1）①如图2中，

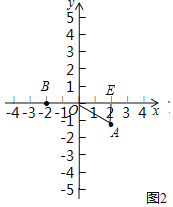
观察图象可知DAO＝2＋1＝3，DBO＝2，

故答案为3，2．

②如图3中，由题意，当DCO为定值时，点C的轨迹是以点O为中心的正方形（如左边图），

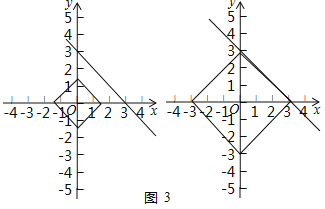
当DCO＝3时，该正方形的一边与直线y＝－x＋3重合（如右边图），

此时DCO定值最小，最小值为3．

（2）如图4中，

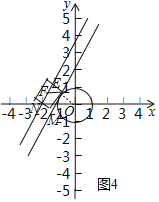
平移直线y＝2x＋4，当平移后的直线与⊙O在左边相切时，设切点为E，作EF∥x轴交直线y＝2x＋4于F，此时DEF定值最小，

因为直线y＝2x＋4与x轴交于N（－2，0），平移后的直线交x轴于M（，0），

∴ON＝2，，

∴.