Question

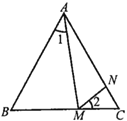
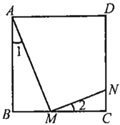
【题目】问题发现：如图，在中，，为边所在直线上的动点(不与点、重合)，连结，以为边作，且，根据，得到，结合，得出，发现线段与的数量关系为，位置关系为；

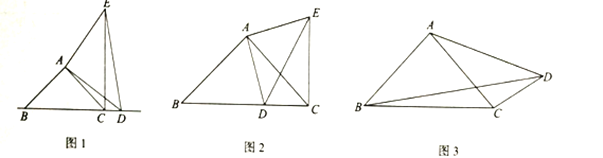
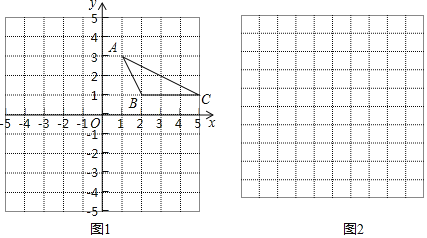
（1）探究证明：如图，在和中，，，且点在边上滑动(点不与点、重合)，连接．

①则线段，，之间满足的等量关系式为_____；

②求证: ；

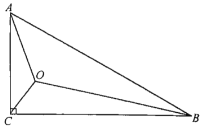
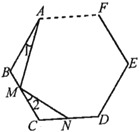
（2）拓展延伸：如图，在四边形中，．若，，求的长．

Answer 1

【答案】（1）①BC =CE+CD；②见解析；（2）AD＝6．

【解析】

（1）①根据题中示例方法，证明△BAD≌△CAE，得到BD＝CE，从而得出BC=CE+CD；

②根据△BAD≌△CAE，得出∠ACE＝45°，从而得到∠BCE＝90°，则有DE2＝CE2+CD2，再根据可得结论；

（2）过点A作AG⊥AD，使AG=AD，连接CG、DG，可证明△BAD≌△CAG，得到CG＝BD，在直角△CDG中，根据CD的长求出DG的长，再由DG和AD的关系求出AD.

解：（1）①如图2，在Rt△ABC中，AB＝AC，

∴∠B＝∠ACB＝45°，

∵∠BAC＝∠DAE＝90°，

∴∠BAC﹣∠DAC＝∠DAE﹣∠DAC，即∠BAD＝∠CAE，

在△BAD和△CAE中，

，

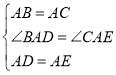∴△BAD≌△CAE（SAS），

∴BD＝CE，

∴ BC=BD+CD=CE+CD，

故答案为：BC=BD+CD=CE+CD．

②∵△BAD≌△CAE，

∴∠B＝∠ACE＝45°，

∵∠ACB＝45°，

∴∠BCE＝45°+45°＝90°，

∴DE2＝CE2+CD2，

∵AD＝AE，∠DAE＝90°，

∴，

∴2AD2＝BD2+CD2；

（3）如图3，

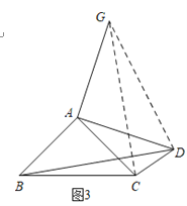
过点A作AG⊥AD，使AG=AD，连接CG、DG，

则△DAG是等腰直角三角形，

∴∠ADG＝45°，

∵∠ADC＝45°，

∴∠GDC＝90°，

同理得：△BAD≌△CAG，

∴CG＝BD＝13，

在Rt△CGD中，∠GDC＝90°，

，

∵△DAG是等腰直角三角形，

∴，

∴AD＝＝6．