题目内容
【题目】问题情境
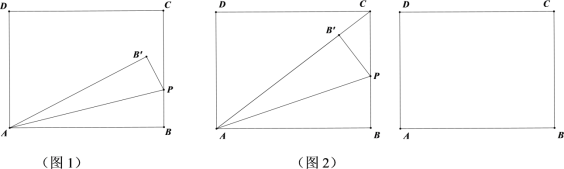
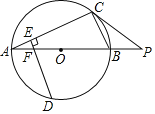
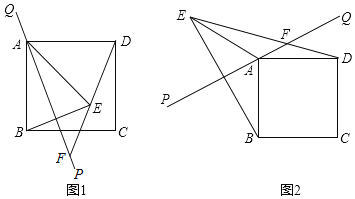
在综合实践课上,同学们以“正方形和直线的旋转”为主题分组开展数学探究活动,已知正方形ABCD,直线PQ经过点A,并绕点A旋转,作点B关于直线PQ的对称点E,直线DE交直线PQ于点F,连结AE,BE.

操作发现
(1)如图1,设∠PAB=25°则∠ADF= °.
(2)“梦想小组”的同学们发现,∠BEF的度数是一个定值,这个值为 .
(3)“创新小组”的同学们发现,线段AB、DF、EF之间存在特殊的数量关系,请写出这一关系式,并说明理由:
拓展应用
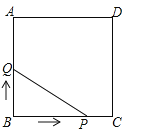
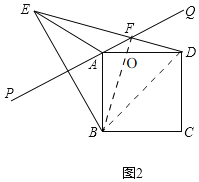
(4)如图2,当直线PQ在正方形ABCD的外部时,“进取小组”的同学们发现(3)的结论仍然成立,并提出新问题;若DF=3![]() ,EF=4
,EF=4![]() ,直接写出正方形ABCD的边长.
,直接写出正方形ABCD的边长.
【答案】(1)70°;(2)45°;(3)EF2+DF2=2AB2,详见解析;(4)5
【解析】
(1)利用折叠得出∠BAP=∠EAP=25°,进而求出∠BAE=50°,即可得出结论;
(2)设∠BAP=α,先求出∠AED=45°+α,再求出∠AEB,即可得出结论;
(3)利用(2)判断出∠BFE=90°,即△BDF是直角三角形,利用勾股定理即可得出结论;
(4)先判断出∠AED=∠ABF,再判断出∠AED=∠ADE,即可得出∠BFD=90°,即可得出结论.
解:(1)∵∠PAB=25°,
由折叠知,∠PAB=∠EAP=25°,
∴∠BAE=50°,
∵四边形ABCD是正方形,
∴∠BAD=90°,
∴∠DAE=40°,
∴∠ADF=![]() (180°﹣40°)=70°
(180°﹣40°)=70°
(2)设∠BAP=α,
由折叠知,AE=AD,∠EAF=∠BAF=α,
∵四边形ABCD是正方形,
∴AB=AD,∠BAD=90°,
∴AD=AE,∠DAE=90°﹣∠BAE=90°﹣2α,
∴∠AED=![]() (180°﹣∠DAE)=90°﹣
(180°﹣∠DAE)=90°﹣![]() ∠DAE=90°﹣
∠DAE=90°﹣![]() (90°﹣2α)=45°+α,
(90°﹣2α)=45°+α,
由折叠知,BE⊥AP,
∴∠AEB+∠EAF=90°,
∴∠AEB=90°﹣∠EAF=90°﹣α,
∴∠BEF=180°﹣∠AEB﹣∠AED=180°﹣(90°﹣α)﹣(45°+α)=45°,
故答案为:45°;
(3)EF2+DF2=2AB2;
理由:如图1,连接BF,
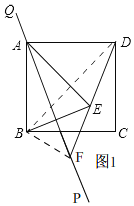
由折叠知,BF=EF,∠BEF=∠EBF,
由(2)知,∠BEF=45°,
∴∠BFE=90°,
连接BD,
∴△BDF是直角三角形,
∴BD2=BF2+DF2=EF2+DF2,
∵BD是正方形ABCD的对角线,
∴BD2=2AB2,
∴EF2+DF2=2AB2;
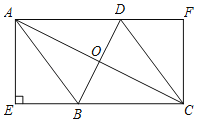
(4)如图2,连接BD,BF,
由折叠知,∠BEF=∠EBF,∠AEB=∠ABE,
∴∠AED=∠ABF,
由折叠知,EF=BF,AE=AB,
∵四边形ABCD是正方形,
∴∠BAD=90°,AB=AD,
∴AE=AD,
∴∠AED=∠ADE,
∴∠ABF=∠ADE,
∵∠AOB=∠FOD,
∴∠BFD=∠BAD=90°
∴△BDF是直角三角形,
∴BD2=BF2+DF2=EF2+DF2,
∵BD是正方形ABCD的对角线,
∴BD2=2AB2,
∴EF2+DF2=2AB2,
∵DF=![]() ,EF=
,EF=![]() ,
,
∴2AB2=32+18=50,
∴AB=5
即:正方形ABCD的边长为5.

 阅读快车系列答案
阅读快车系列答案