��Ŀ����
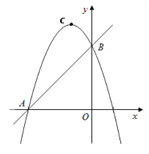
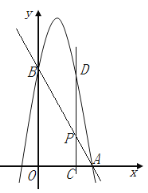
����Ŀ����ͼ1���ھ���ABCD�У�BC=3������P��B��������ÿ��1����λ���ٶȣ�������BC�����ƶ�������PAB����ֱ��PA�ĶԳơ�PAB' �����P���˶�ʱ��Ϊt��s����
��1����AB=2![]() ��
��
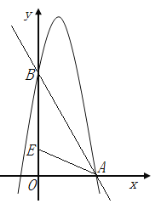
����ͼ2������B' ����AC��ʱ����t��ֵ��
���Ƿ��������ͼ2��ʱ�̣�ʹ�á�PCB����ֱ�������Σ������ڣ���ֱ��д�����з��������tֵ���������ڣ���˵������.
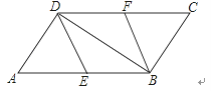
��2�����ı���ABCD�������Σ�ֱ��PB'��ֱ��CD�ཻ�ڵ�M������P�����C�غ�ʱ����֤����PAM=45��.
���𰸡���1����t=2![]() ��4���ڴ��ڣ�t=2��t=6��t=2
��4���ڴ��ڣ�t=2��t=6��t=2![]() ����2���������
����2���������
��������
��1�������ù��ɶ������AC������PCB���ס�ACB���Ƴ�![]() ���ɽ�����⣮
���ɽ�����⣮
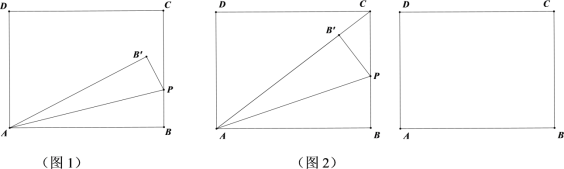
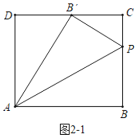
�ڷ��������ηֱ���⼴�ɣ���ͼ2-1�У�����PCB��=90��ʱ����ͼ2-2�У�����PCB��=90��ʱ����ͼ2-3�У�����CPB��=90��ʱ��
��2����ͼ3-1�У���t<3ʱ�����ı���ABCD�������Σ�֤����MDA�ա�MB��A�����ɵõ���������ͼ3-2�У���t>3ʱ�����APB=x������ȫ�������ε����ʣ����۲����Լ��ɽ�����⣮
�⣺��1������ͼ1�У�
���ı���ABCD�Ǿ��Σ�
���ABC=90���� ��![]()
�ߡ�PCB��=��ACB����PB��C=��ABC=90����
���PCB���ס�ACB��
��![]()
�� ![]()
��![]()
��![]()
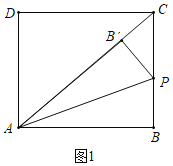
����ͼ2-1�У�����PCB��=90��ʱ��
���ı���ABCD�Ǿ��Σ� ���D=90����AB=CD=![]() AD=BC=3��
AD=BC=3��
��![]()
��![]()
��Rt��PCB������![]()
��![]()
��![]()
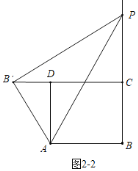
��ͼ2-2�У�����PCB��=90��ʱ��
��Rt��ADB����![]() ��
��
![]()
��Rt��PCB��������![]()
���t=6��
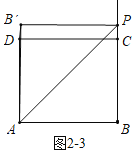
��ͼ2-3�У�����CPB��=90��ʱ����![]()
���ı���![]() Ϊ�����Σ�
������
![]()
![]()
��������������������t��ֵΪ2s��6s��![]() s��
s��
��2����ͼ3-1����t<3ʱ��
�֡߷��ۣ�
���1=��2��AB=AB������B=��AB��P
���ı���ABCD�������Σ�
��AD=AB=AB�� ����D=��B=��AB��P= 90��
��AM=AM
���MDA�ա�MB��A��HL��
���3=��4
���2+��3=45����
����PAM=45��
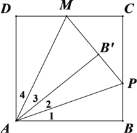
��������ͼ3-1��
��ͼ3-2����t>3ʱ�����APB=x
���PAB=90����x
���DAP��x
ͬ������MDA�ա�MB��A��HL��
���B��AM����DAM
�߷���
���PAB����PAB����90����x
���DAB������PAB������DAP��90����2x
���DAM��![]() ��DAB����45����x
��DAB����45����x
���MAP=��DAM+��PAD=45��
��ͼ3-2��

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�����Ŀ������ʦΪ�˽����ν̵��������ѧ����ѧѧϰ���������ѧ������һ�β��ԣ������������ijɼ����ٷ��ƣ����������ݣ��ɼ������������������ͷ�������������˲�����Ϣ��
��A��B����ѧ�����������������ͬ����ѧ�ɼ���������Ƶ���ֲ�ֱ��ͼ���£����ݷֳ�5�飺x<60��60��x<70��70��x<80��80��x<90��90��x��100����
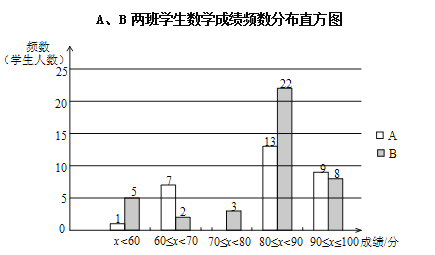
��A��B����ѧ�����Գɼ���80��x<90��һ����������£�
A�ࣺ80 80 82 83 85 85 86 87 87 87 88 89 89
B�ࣺ80 80 81 81 82 82 83 84 84 85 85 86 86 86 87 87 87 87 87 88 88 89
��A��B����ѧ�����Գɼ���ƽ��������λ�����������£�
ƽ���� | ��λ�� | ���� | |
A�� | 80.6 | m | 96.9 |
B�� | 80.8 | n | 153.3 |
����������Ϣ���ش��������⣺
��1����ȫ��ѧ�ɼ�Ƶ���ֲ�ֱ��ͼ��
��2��д������m��n��ֵ��
��3������Աȷ���A��B����ѧ������ѧѧϰ��������ٴ�������ͬ�ĽǶȷ�������