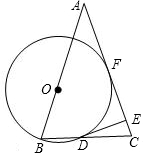
题目内容
如图,在Rt△ABC中,∠C=90°,AC=12,BC=16.∠BAC的平分线AD交BC于D,经过A、D两点的⊙O交AB 于E,且点O在AB上.
于E,且点O在AB上.
(1)求证:BC是⊙O的切线;
(2)求AF的长.
 于E,且点O在AB上.
于E,且点O在AB上.(1)求证:BC是⊙O的切线;
(2)求AF的长.
(1)证明:连接OD,
∵OA=OD,
∴∠OAD=∠ODA.(1分)
∵AD平分∠BAC,
∴∠OAD=∠CAD.(2分)
∴OD∥AC.(3分)
∵∠C=90°,
∴OD⊥BC于D.
∴BC是⊙O的切线.(4分)
(2)过D作DG⊥AB于G,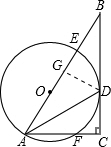
∴DG=DC,AG=AC.(5分)
设DC=x,则BD=16-x,BG=8,
∴82+x2=(16-x)2
∴x=6.(6分)
设半径为r,则(12-r)2+62=r2
∴r=7.5.
∴EG=3.(7分)
连接DE,DF,易证△DGE≌△DCF,
∴CF=3,
∴AF=9.(8分)
(2)证法2:(如图)连OD,OF,作OM⊥AF于M;
设DC=x,(x的求法同于前面)
∴x=6;
∵OM⊥AF,OD⊥BC,则MC=OD=R,OM=DC=6,AM=12-R,
∴R2=(12-R)2+62,
∴R=7.5,
∴AM=12-7.5=4.5,
∴AF=2AM=9.
证法3:(如图)连EF,与OD交于H点,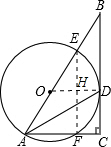 设DC=x
设DC=x
∴x=6,(求法同前);
在Rt△BOD中,BO=20-R,OD=R,BD=10;
∴(20-R)2=R2+102,
∴R=7.5,
∴AE=15;
∵EF=2FH=2CD=12,
在Rt△EAF中,AF2=AE2-EF2=152-122=81,
∴AF=9.
证法4,(如图)连EF;设DC=x,
∴x=6,(求法同前)
∴EF=2FH=2CD=12;
∵S△BEF+S梯形EFCB=S△ABC,
EF•BF+
(EF+BC)•(AC-AF)=
AC•BC,
∴AF=9.
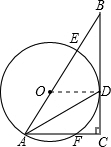
∵OA=OD,
∴∠OAD=∠ODA.(1分)
∵AD平分∠BAC,
∴∠OAD=∠CAD.(2分)
∴OD∥AC.(3分)
∵∠C=90°,
∴OD⊥BC于D.
∴BC是⊙O的切线.(4分)
(2)过D作DG⊥AB于G,

∴DG=DC,AG=AC.(5分)
设DC=x,则BD=16-x,BG=8,
∴82+x2=(16-x)2
∴x=6.(6分)
设半径为r,则(12-r)2+62=r2
∴r=7.5.
∴EG=3.(7分)
连接DE,DF,易证△DGE≌△DCF,
∴CF=3,
∴AF=9.(8分)
(2)证法2:(如图)连OD,OF,作OM⊥AF于M;

设DC=x,(x的求法同于前面)
∴x=6;
∵OM⊥AF,OD⊥BC,则MC=OD=R,OM=DC=6,AM=12-R,
∴R2=(12-R)2+62,
∴R=7.5,
∴AM=12-7.5=4.5,
∴AF=2AM=9.
证法3:(如图)连EF,与OD交于H点,
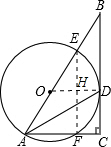 设DC=x
设DC=x∴x=6,(求法同前);
在Rt△BOD中,BO=20-R,OD=R,BD=10;
∴(20-R)2=R2+102,
∴R=7.5,
∴AE=15;
∵EF=2FH=2CD=12,
在Rt△EAF中,AF2=AE2-EF2=152-122=81,
∴AF=9.
证法4,(如图)连EF;设DC=x,
∴x=6,(求法同前)
∴EF=2FH=2CD=12;
∵S△BEF+S梯形EFCB=S△ABC,
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴AF=9.


练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

 AC交BC于点D,在OD的延长线上取一点E,连接EB,使∠OEB=∠ABC.
AC交BC于点D,在OD的延长线上取一点E,连接EB,使∠OEB=∠ABC.
 接AB,过O1作O1C⊥BA于C,连接CO2.已知PA=
接AB,过O1作O1C⊥BA于C,连接CO2.已知PA=