题目内容
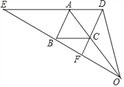
【题目】如图所示，A（﹣
，0）、B（0，1）分别为x轴、y轴上的点，△ABC为等边三角形，点P（3，a）在第一象限内，且满足2S△ABP=S△ABC，则a的值为（ ）
A.
B.
C.D.2
【答案】C
【解析】
过P点作PD⊥x轴，垂足为D，根据A（
，0）、B（0，1）求OA、OB，利用勾股定理求AB，可得△ABC的面积，利用S△ABP=S△AOB+S梯形BODP﹣S△ADP，列方程求a．
过P点作PD⊥x轴，垂足为D，由A（，0）、B（0，1），得OA
，OB=1．
∵△ABC为等边三角形，由勾股定理，得AB
2，∴S△ABC
．
又∵S△ABP=S△AOB+S梯形BODP﹣S△ADP
（1+a）×3
（
3）×a=
由2S△ABP=S△ABC，得：
，∴a．
故选C．
练习册系列答案
相关题目
【题目】某校八年级所有女生的身高统计数据如下表，请回答下列问题：
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1) 这个学校八年级共有多少女生？
(2) 身高在 
到 
的女生有多少人？
(3) 一女生的身高恰好为 
，哪一组包含这个身高？这一组出现的频数、频率各是多少？