ЬтФПФкШн
ЁОЬтФПЁПвбжЊЃКЙигкxЕФвЛдЊЖўДЮЗНГЬax2Љ2ЃЈaЉ1ЃЉx+aЉ2=0ЃЈaЃО0ЃЉЃЎ
ЃЈ1ЃЉЧѓжЄЃКЗНГЬгаСНИіВЛЯрЕШЕФЪЕЪ§ИљЃЛ
ЃЈ2ЃЉЩшЗНГЬЕФСНИіЪЕЪ§ИљЗжБ№ЮЊx1ЃЌx2ЃЈЦфжаx1ЃОx2ЃЉЃЎШєyЪЧЙигкaЕФКЏЪ§ЃЌЧвy=ax2x1ЃЌЧѓетИіКЏЪ§ЕФБэДяЪНЃЛ
ЃЈ3ЃЉНЋЃЈ2ЃЉжаЫљЕУЕФКЏЪ§ЕФЭМЯѓдкжБЯпa=2ЕФзѓВрВПЗжбижБЯпa=2ЗелЃЌЭМЯѓЕФЦфгрВПЗжБЃГжВЛБфЃЌЕУЕНвЛИіаТЕФЭМЯѓЃЎЧыФуНсКЯетИіаТЕФЭМЯѓжБНгаДГіЃКЕБЙигкaЕФКЏЪ§y=2a+bЕФЭМЯѓгыДЫЭМЯѓгаСНИіЙЋЙВЕуЪБЃЌbЕФШЁжЕЗЖЮЇЪЧЁЁЁЁЃЎ
ЁОД№АИЁПЃЈ1ЃЉМћНтЮіЃЛЃЈ2ЃЉy=aЉ3ЃЈaЃО0ЃЉЃЛЃЈ3ЃЉЉ11ЃМbЃМЉ5
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнвЛдЊЖўДЮЗНГЬЕФИљЕФХаБ№ЪНХаЖЯМДПЩЃЛ
ЃЈ2ЃЉЯШИљОнвЛдЊЖўДЮЗНГЬЕФЧѓИљЙЋЪНЕУГіx1ЃЌx2ЃЌМДПЩЕУГіКЏЪ§КЏЪ§ЙиЯЕЪНЃЛ
ЃЈ3ЃЉЛГіаТКЏЪ§ЕФЭМаЮКЭжБЯпy=2a+bЃЌРћгУЭМаЮКЭжБЯпгыyжсЕФНЛЕузјБъМДПЩЕУГіНсТлЃЎ
ЃЈ1ЃЉжЄУїЃКЁпax2Љ2ЃЈaЉ1ЃЉx+aЉ2=0ЃЈaЃО0ЃЉЪЧЙигкxЕФвЛдЊЖўДЮЗНГЬЃЌ
ЁрЁї=[Љ2ЃЈaЉ1ЃЉ]2Љ4aЃЈaЉ2ЃЉ=4ЃО0ЃЌ
ЁрЗНГЬax2Љ2ЃЈaЉ1ЃЉx+aЉ2=0ЃЈaЃО0ЃЉгаСНИіВЛЯрЕШЕФЪЕЪ§ИљЃЎ
ЃЈ2ЃЉНтЃКгЩЧѓИљЙЋЪНЃЌЕУx=![]() ЃЎ
ЃЎ
Ёрx=1Лђx=1Љ![]() ЃЎ
ЃЎ
ЁпaЃО0ЃЌx1ЃОx2ЃЌ
Ёрx1=1ЃЌx2=1Љ![]() ЃЌ
ЃЌ
Ёрy=ax2x1=aЁСЃЈ1Љ![]() ЃЉЉ1=aЉ3ЃЎ
ЃЉЉ1=aЉ3ЃЎ
МДКЏЪ§ЕФБэДяЪНy=aЉ3ЃЈaЃО0ЃЉЃЌ
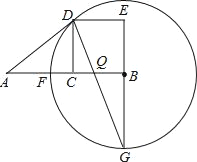
ЃЈ3ЃЉНтЃКШчЭМЃЌжБЯпBDИеКУКЭелЯпCBAжЛгавЛИіЙЋЙВЕуЃЌдйЯђЯТЦНвЦЃЌОЭКЭетаЉCBAгаСНИіЙЋЙВЕуЃЌ
МЬајЯђЯТЦНвЦЕНжБЯпCEЕФЮЛжУКЭжБЯпCBAИеКУга1ИіЙЋЙВЕуЃЌдйЯђЯТЦНвЦКЭетаЉCBAвВжЛгавЛИіЙЋЙВЕуЃЌ
гЩЃЈ2ЃЉжЊЃЌКЏЪ§ЕФБэДяЪНy=aЉ3ЃЈaЃО0ЃЉЃЌ
ЕБa=2ЪБЃЌy=2Љ3=Љ1ЃЌ
ЁрBЃЈ2ЃЌЉ1ЃЉЃЌ
гЩелЕўЕУЃЌCЃЈ4ЃЌЉ3ЃЉЃЌ
ЕБКЏЪ§y=2a+bЕФЭМЯѓЙ§ЕуBЪБЃЌ
ЁрЉ1=2ЁС2+bЃЌ
Ёрb=Љ5ЃЌ
ЕБКЏЪ§y=2a+bЕФЭМЯѓЙ§ЕуCЪБЃЌ
ЁрЉ3=2ЁС4+bЃЌ
Ёрb=Љ11ЃЌ
ЁрЉ11ЃМbЃМЉ5ЃЎ
ЙЪД№АИЮЊЃКЉ11ЃМbЃМЉ5ЃЎ


 ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ
ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИЁОЬтФПЁПвдЯТЪЧАЫЃЈ1ЃЉАрбЇЩњЩэИпЕФЭГМЦБэКЭЩШаЮЭГМЦЭМЃЌЧыЛиД№вдЯТЮЪЬт.
АЫЃЈ1ЃЉАрбЇЩњЩэИпЭГМЦБэ
зщБ№ | ЩэИпЃЈЕЅЮЛЃКУзЃЉ | ШЫЪ§ |
ЕквЛзщ | 1.85вдЩЯ | 1 |
ЕкЖўзщ |
| |
ЕкШ§зщ |
| 19 |
ЕкЫФзщ |
| |
ЕкЮхзщ | 1.55вдЯТ | 8 |

ЃЈ1ЃЉЧѓГіЭГМЦБэКЭЭГМЦЭМШБЕФЪ§Он.
ЃЈ2ЃЉАЫЃЈ1ЃЉАрбЇЩњЩэИпетзщЪ§ОнЕФжаЮЛЪ§ТфдкЕкМИзщЃП
ЃЈ3ЃЉШчЙћЯждкАЫЃЈ1ЃЉАрбЇЩњЕФЦНОљЩэИпЪЧ1.63 ![]() ЃЌвбШЗЖЈаТбЇЦкАрМЖзЊРДСНУћаТЭЌбЇЃЌаТЭЌбЇЕФЩэИпЗжБ№ЪЧ1.54
ЃЌвбШЗЖЈаТбЇЦкАрМЖзЊРДСНУћаТЭЌбЇЃЌаТЭЌбЇЕФЩэИпЗжБ№ЪЧ1.54 ![]() КЭ1.77
КЭ1.77 ![]() ЃЌФЧУДетзщаТЪ§ОнЕФжаЮЛЪ§ТфдкЕкМИзщЃП
ЃЌФЧУДетзщаТЪ§ОнЕФжаЮЛЪ§ТфдкЕкМИзщЃП
ЁОЬтФПЁПФГЩЬГЁЯњЪлвЛХњНјМлЮЊ10дЊЕФаТЩЬЦЗЃЌЮЊбАЧѓКЯЪЪЕФЯњЪлМлИёЃЌЫћУЧНјааСЫ4ЬьЕФЪдЯњЃЌЪдЯњЧщПіШчЯТБэЃК
Ек1Ьь | Ек2Ьь | Ек3Ьь | Ек4Ьь | |
ШеЯњЪлЕЅМлxЃЈдЊЃЉ | 20 | 30 | 40 | 50 |
ШеЯњЪлСПyЃЈИіЃЉ | 300 | 200 | 150 | 120 |
ЃЈ1ЃЉИљОнЪдЯњЧщПіЃЌЧыФуВТВтВЂЧѓГіyгыxжЎМфЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ2ЃЉШєИУЩЬГЁМЦЛЎУПЬьЯњЪлетжжЩЬЦЗЕФРћШѓвЊДяЕН3600дЊЃЌЮЪИУЩЬЦЗЯњЪлЕЅМлгІЖЈЮЊЖрЩйдЊЃП