题目内容
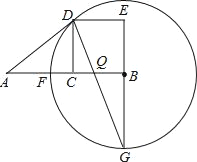
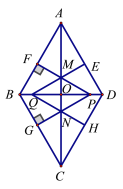
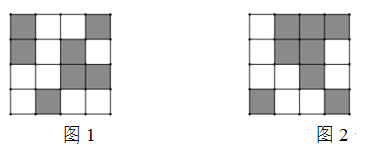
【题目】某校利用二维码进行学生学号统一编排.黑色小正方形表示1,白色小正方形表示0,将每一行数字从左到右依次记为a,b,c,d,那么利用公式a×23-b×22-c×21+d计算出每一行的数据.第一行表示年级,第二行表示班级,如图1所示,第一行数字从左往右依次是1,0,0,1,则表示的数据为1×23+0×22+0×21+1=9,计作09,第二行数字从左往右依次是1,0,1,0,则表示的数据为1×23+0×22+1×21=10,计作10,以此类推,图1代表的统一学号为091034,表示9年级10班34号.小明所对应的二维码如图2所示,则他的编号是_______.
【答案】070629.
【解析】
利用公式求出图2中每行表示的数据,将其组合起来即可得出结论.
解:由图2可知:第一行数字从左往右依次是0,1,1,1,则表示的数据为0×23+1×22+1×21+1=7,计作07,
第二行数字从左往右依次是0,1,1,0,则表示的数据为0×23+1×22+1×21=6,计作06,
第三行数字从左往右依次是0,0,1,0,则表示的数据为0×23+0×22+1×21=2,计作2,
第四行数字从左往右依次是1,0,0,1,则表示的数据为1×23+0×22+0×21+1=9,计作9.
∴图2代表的统一学号为070629.
故答案为:070629.

 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案【题目】利民商场经营某种品牌的T恤,购进时的单价是300元,根据市场调查:在一段时间内,销售单价是400元时,销售量是60件,销售单价每涨10元,销售量就减少1件.设这种T恤的销售单价为x元(x>400)时,销售量为y件、销售利润为W元.
(1)请分别用含x的代数式表示y和W(把结果填入下表):
销售单价(元) | x |
销售量y(件) | |
销售利润W(元) |
(2)该商场计划实现销售利润10000元,并尽可能增加销售量,那么x的值应当是多少?
【题目】某商场销售一批进价为10元的新商品,为寻求合适的销售价格,他们进行了4天的试销,试销情况如下表:
第1天 | 第2天 | 第3天 | 第4天 | |
日销售单价x(元) | 20 | 30 | 40 | 50 |
日销售量y(个) | 300 | 200 | 150 | 120 |
(1)根据试销情况,请你猜测并求出y与x之间的函数关系式;
(2)若该商场计划每天销售这种商品的利润要达到3600元,问该商品销售单价应定为多少元?
【题目】某服装店用6000元购进A,B两种新式服装,按标价售出后可获得毛利润3800元(毛利润=售价﹣进价),这两种服装的进价、标价如下表所示:
类型 价格 | A型 | B型 |
进价(元/件) | 60 | 100 |
标价(元/件) | 100 | 160 |
(1)求这两种服装各购进的件数;
(2)如果A中服装按标价的8折出售,B中服装按标价的7折出售,那么这批服装全部售完后,服装店比按标价售出少收入多少元?