题目内容
已知P（x1，y1）、Q（x2，y2）是直角坐标系第一象限内的点，给出下列说法：①P、Q必定在同一抛物线上；②P、Q必定在同一双曲线上；③P、Q必定在同一直线上．其中正确的个数是（ ）A．3个
B．2个
C．1个
D．0个
【答案】分析：根据函数图象上的点的坐标满足函数解析式，结合抛物线解析式，双曲线的解析式，直线的解析式进行分析判断即可．
解答：解：①如果x1与x2的横坐标相同，那么P（x1，y1）、Q（x2，y2）不能在同一抛物线上，故本小题错误；
②∵双曲线的解析式为y=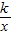
，∴适合点P的常数k值不一定适合点Q，
即：P、Q不一定在同一双曲线上，故本小题错误；
③∵两点确定一条直线，∴P、Q必定在同一直线上，故本小题正确．
综上所述，③正确．
故选C．
点评：本题主要考查了二次函数图象上点的坐标的特征，反比例函数图象上的点的坐标的特征，一次函数图象上的点的坐标的特征，根据系数的数量进行判断是解题的关键．
解答：解：①如果x1与x2的横坐标相同，那么P（x1，y1）、Q（x2，y2）不能在同一抛物线上，故本小题错误；
②∵双曲线的解析式为y=
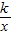，∴适合点P的常数k值不一定适合点Q，即：P、Q不一定在同一双曲线上，故本小题错误；
③∵两点确定一条直线，∴P、Q必定在同一直线上，故本小题正确．
综上所述，③正确．
故选C．
点评：本题主要考查了二次函数图象上点的坐标的特征，反比例函数图象上的点的坐标的特征，一次函数图象上的点的坐标的特征，根据系数的数量进行判断是解题的关键．
练习册系列答案
相关题目
已知P1（x1，y1），P2（x2，y2），P3（x3，y3）是反比例函数y=
的图象上的三点，且x1＜x2＜0＜x3，则y1、y2、y3的大小关系是（ ）
| 2 |
| x |
| A、y3＜y2＜y1 |
| B、y1＜y2＜y3 |
| C、y2＜y1＜y3 |
| D、y2＜y3＜y1 |
已知A（x1，y1）、B（x2，y2）都是函数y=
(k＞0)图象上的点，且x1＜x2＜0，则y1、y2的大小是（ ）
| k |
| x |
| A、y1＜y2 |
| B、y1=y2 |
| C、y1＞y2 |
| D、不能确定 |