Question

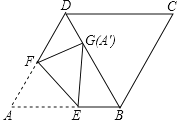
【题目】如图，四边形ABCD为菱形，M为BC上一点，连接AM交对角线BD于点G，并且∠ABM=2∠BAM．

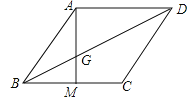
（1）求证：AG=BG；

（2）若点M为BC的中点，同时S△BMG=1，求三角形ADG的面积．

Answer 1

【答案】（1）证明见试题解析；（2）4．

【解析】

试题（1）由菱形的对角线平分一组对角，得出∠ABD=∠CBD，再由∠ABM=2∠BAM，得出∠ABD=∠BAM，即可得出结论．

（2）由相似三角形面积的比等于相似比的平方即可求得．

试题解析：（1）∵四边形ABCD是菱形，∴∠ABD=∠CBD，∵∠ABM=2∠BAM，∴∠ABD=∠BAM，∴AG=BG；

（2）∵AD∥BC，∴△ADG∽△MBG，∴，∵点M为BC的中点，∴=2，∴=4，∵S△BMG=1，∴S△ADG=4．