题目内容
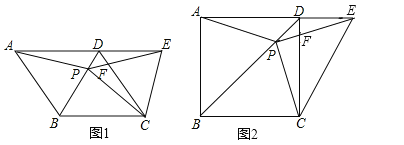
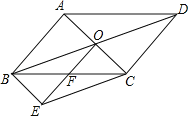
【题目】如图，四边形ABCD是平行四边形，以点A为圆心、AB的长为半径画弧交AD于点F，再分别以点B，F为圆心、大于
BF的长为半径画弧，两弧交于点M，作射线AM交BC于点E，连接EF．下列结论中不一定成立的是（ ）
A. BE＝EFB. EF∥CDC. AE平分∠BEFD. AB＝AE
【答案】D
【解析】
首先证明四边形ABEF是菱形，利用菱形的性质对各个选项进行判断即可．
由尺规作图可知：AF＝AB，AE平分∠BAD，
∴∠BAE＝∠DAE，
∵四边形ABCD是平行四边形，
∴AD∥BC，
∴∠DAE＝∠BEA．
∴∠BAE＝∠BEA，
∴AB＝BE，
∵AF＝AB，
∴AF＝BE，
∵AF∥BE，
∴四边形ABEF是平行四边形，
∵AF＝AB，
∴四边形ABEF是菱形，
∴AE平分∠BEF，BE＝EF，EF∥AB，故选项A、C正确，
∵CD∥AB，
∴EF∥CD，故选项B正确；
故选：D．
灵星计算小达人系列答案
孟建平错题本系列答案
【题目】某企业为了解饮料自动售卖机的销售情况，对甲、乙两个城市的饮料自动售卖机进行了抽样调查，从两个城市中所有的饮料自动售卖机中分别随机抽取16台，记录下某一天各自的销售情况（单位：元）如下：
甲：25，45，44，22，10，28，61，18，38，45，78，45，58，32，16，72
乙：48，52，21，25，33，12，42，39，41，42，33，44，33，18，68，72
整理、描述数据，对销售金额进行分组，各组的频数如下：
销售金额 |
|
|
|
|
甲 | 3 | 5 | 5 | 3 |
乙 | 2 | 6 |
|
|
分析数据，两组样本数据的平均数、中位数如下表所示：
城市 | 中位数 | 平均数 | 众数 |
甲 |
| 39.8 | 45 |
乙 | 40 | 38.9 |
|
请根据以上信息，回答下列问题：
（1）填空：
________，
________，
________，
________
（2）两个城市目前共有饮料自动售卖机4000台，估计日销售金额不低于40元的数量约为多少台？
（3）根据以上数据，你认为甲、乙哪个城市的饮料自动售卖机销售情况较好？请说明理由（一条理由即可）．
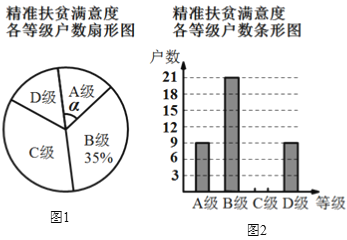
【题目】中华文明，源远流长；中华诗词，寓意深广．为了传承优秀传统文化，我市某校团委组织了一次全校2000名学生参加的“中国诗词大会”海选比赛，赛后发现所有参赛学生的成绩均不低于50分，为了更好地了解本次海选比赛的成绩分布情况，随机抽取了其中200名学生的海选比赛成绩（成绩x取整数，总分100分）作为样本进行整理，得到下列统计图表：
抽取的200名学生海选成绩分组表
组别 | 海选成绩x |
A组 | 50≤x＜60 |
B组 | 60≤x＜70 |
C组 | 70≤x＜80 |
D组 | 80≤x＜90 |
E组 | 90≤x＜100 |
请根据所给信息，解答下列问题：
（1）请把图1中的条形统计图补充完整；（温馨提示：请画在答题卷相对应的图上）
（2）在图2的扇形统计图中，记表示B组人数所占的百分比为a%，则a的值为 ，表示C组扇形的圆心角θ的度数为 度；
（3）规定海选成绩在90分以上（包括90分）记为“优等”，请估计该校参加这次海选比赛的2000名学生中成绩“优等”的有多少人？
