题目内容
【题目】如图,△ABC中,∠C=90°,AC=6,BC=8,动点P从A点出发,以1cm/s的速度,沿A—C—B向B点运动,同时,动点Q从C点出发,以2cm/s的速度,沿C—B—A向A点运动,当其中一点运动到终点时,两点同时停止运动。设运动时间为t秒,当t=_______秒时,△PCQ的面积等于8cm2.

【答案】2或4或![]()
【解析】设经过t秒钟,△PCQ的面积等于8.
①当0<t≤4时,P在AC上,Q在BC上,则PC=6-t,CQ=2t.
∴△PCQ的面积=![]() PCCQ=
PCCQ=![]() ,解得:t=2或t=4.
,解得:t=2或t=4.
②当4<t≤6时,P在AC上,Q在AB上,如图,∵AC=6,BC=8,∴AC=10.过Q作QH⊥AC于H,则PC=6-t,BQ=2t-8,AQ=18-2t.∵QH∥BC,∴ ![]() ,∴
,∴![]() ,解得:QH=0.8(18-2t),∴△PCQ的面积=
,解得:QH=0.8(18-2t),∴△PCQ的面积=![]() PCQH=
PCQH=![]() ,解得:t=4或t=11.∵4<t≤6,故两个答案都舍去.
,解得:t=4或t=11.∵4<t≤6,故两个答案都舍去.
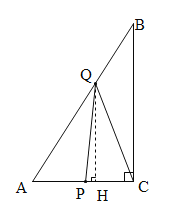
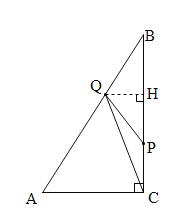
③当6<t≤8时, P在BC上,Q在AB上,如图,∵AC=6,BC=8,∴AC=10.过Q作QH⊥BC于H,则PC=t-6,BQ=2t-8,AQ=18-2t.∵QH∥AC,∴ ![]() ,∴
,∴![]() ,解得:QH=0.6(2t-8),∴△PCQ的面积=
,解得:QH=0.6(2t-8),∴△PCQ的面积=![]() PCQH=
PCQH=![]() ,解得:t=
,解得:t=![]() 或t=
或t=![]() .∵6<t≤8,故t=
.∵6<t≤8,故t=![]() .
.
故答案为:2或4或![]() .
.

练习册系列答案
相关题目