题目内容
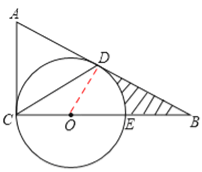
【题目】如图,在△ABC中,∠ACB=90°,E为BC上一点,以CE为直径作⊙O,AB与⊙O相切于点D,连接CD,若BE=OE=2.
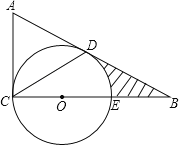
(1)求证:∠A=2∠DCB;
(2)求图中阴影部分的面积(结果保留π和根号).
【答案】解:(1)证明:连接OD,
∵AB是⊙O切线,∴∠ODB=90°。
∴BE=OE=OD=2。
∴∠B=30°,∠DOB=60°。
∵OD=OC,∴∠DCB=∠ODC=![]() ∠DOB=30°。
∠DOB=30°。
∵在△ABC中,∠ACB=90°,∠B=30°,
∴∠A=60°。∴∠A=2∠DCB。
(2)∵∠ODB=90°,OD=2,BO=2+2=4,由勾股定理得:BD=2![]() ,
,
∴阴影部分的面积![]()
【解析】
试题(1)连接OD,求出∠ODB=90°,求出∠B=30°,∠DOB=60°,求出∠DCB度数,关键三角形内角和定理求出∠A,即可得出答案。
(2)根据勾股定理求出BD,分别求出△ODB和扇形DOE的度数,即可得出答案。

【题目】列方程组解应用题某校组织“大手拉小手,义卖献爱心”活动,计划购买黑、白两种颜色的文化衫进行手绘设计后出售,并将所获利润全部捐给山区困难孩子.已知该学校从批发市场花2400元购买了黑、白两种颜色的文化衫100件,每件文化衫的批发价及手绘后的零售价如表:
批发价(元) | 零售价(元) | |
黑色文化衫 | 25 | 45 |
白色文化衫 | 20 | 35 |
(1)学校购进黑、白文化衫各几件?
(2)通过手绘设计后全部售出,求该校这次义卖活动所获利润.
【题目】某超市在春节期间对顾客实行优惠,规定如下:
一次性购物 | 优惠办法 |
少于200元 | 不予优惠 |
低于500元但不低于200元 | 九折优惠 |
500元或超过500元 | 其中500元部分给予九折优惠,超过500元部分给予八折优惠 |
(1)王老师一次性购物600元,他实际付款 元.
(2)若顾客在该超市一次性购物x元,当x小于500元但不小于200时,他实际付款 元,当x大于或等于500元时,他实际付款 元.(用含x的代数式表示).
(3)如果王老师两次购物货款合计820元,第一次购物的货款为a元(200<a<300),用含a的代数式表示:两次购物王老师实际付款多少元?