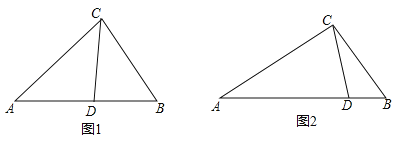题目内容
【题目】已知抛物线y=ax2+bx+c(a≠0)经过原点,
(1)当顶点坐标为(2,2)时,求此函数的解析式;
(2)继续探究,如果b≠0,且抛物线顶点坐标为(m,m),m≠0,求此函数的解析式(用含m的式子表示)
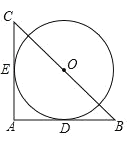
(3)现有一组过原点的抛物线,顶点A1,A2,An在直线y=x上,横坐标依次为1,2,…,n(n为正整数,且n≤12),分别过每个顶点作x轴的垂线,垂足记为B1,B2,…,Bn,以线段AnBn为边向右作正方形AnBnnDn,若这组抛物线中有一条经过Dn,求所有满足条件的正方形边长.
【答案】(1)y=﹣![]() x2+2x;(2)y=﹣
x2+2x;(2)y=﹣![]() x2+2x;(3)满足条件的正方形边长是3,6或9.
x2+2x;(3)满足条件的正方形边长是3,6或9.
【解析】
(1)顶点坐标为(2,2)时,抛物线的表达式为:y=a(x2)2+2=ax24ax+4a+2,故4a+2=0,解得:a=![]() ,即可求解;
,即可求解;
(2)抛物线顶点坐标为(m,m),抛物线的表达式为:y=a(xm)2+m=ax22max+am2+m,即:am2+m=0,解得:a=![]() ,即可求解;
,即可求解;
(3)点Dn所在的抛物线解析式为y=![]() x2+2x.四边形AnBnCnDn是正方形,则点Dn的坐标是(2n,n),
x2+2x.四边形AnBnCnDn是正方形,则点Dn的坐标是(2n,n),![]() (2n)2+22n=n,4n=3t,即可求解.
(2n)2+22n=n,4n=3t,即可求解.
抛物线y=ax2+bx+c(a≠0)经过原点,则抛物线的表达式为:y=ax2+bx;
(1)顶点坐标为(2,2)时,抛物线的表达式为:y=a(x﹣2)2+2=ax2﹣4ax+4a+2,
故4a+2=0,解得:a=﹣![]() ,
,
故抛物线的表达式为:y=﹣![]() (x﹣2)2+2=﹣
(x﹣2)2+2=﹣![]() x2+2x;
x2+2x;
(2)抛物线顶点坐标为(m,m),抛物线的表达式为:y=a(x﹣m)2+m=ax2﹣2max+am2+m,
即:am2+m=0,解得:a=﹣![]() ,
,
故抛物线的表达式为:y=﹣![]() (x﹣m)2+m=﹣
(x﹣m)2+m=﹣![]() x2+2x;
x2+2x;
(3)∵顶点A1,A2,…,An在直线y=x上,
∴可设An(n,n),点Dn所在的抛物线顶点坐标为(t,t).
∴a=﹣![]() x2+2x.
x2+2x.
∵四边形AnBnC nDn是正方形,C
∴点Dn的坐标是(2n,n),
∴﹣![]() (2n)2+22n=n,
(2n)2+22n=n,
∴4n=3t.
∵t、n是正整数,且t≤12,n≤12,
∴n=3,6或9.
∴满足条件的正方形边长是3,6或9.

【题目】小东根据学习函数的经验,对函数![]() 的图象与性质进行了探究.下面是小东的探究过程,请补充完整,并解决相关问题:
的图象与性质进行了探究.下面是小东的探究过程,请补充完整,并解决相关问题:
(1)函数![]() 的自变量x的取值范围是 ;
的自变量x的取值范围是 ;
(2)下表是y与x的几组对应值.
x | … |
|
|
| 0 |
| 1 |
| 2 |
| 3 | 4 | … |
y | … |
|
|
| 2 |
| 4 |
| 2 |
|
| m | … |
表中m的值为________________;
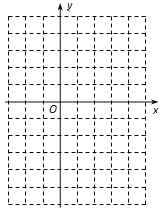
(3)如图,在平面直角坐标系中,描出了以上表中各对对应值为坐标的点. 根据描出的点,画出函数![]() 的大致图象;
的大致图象;
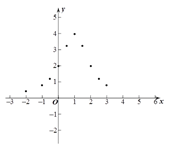
(4)结合函数图象,请写出函数![]() 的一条性质:______________________.
的一条性质:______________________.
(5)解决问题:如果函数![]() 与直线y=a的交点有2个,那么a的取值范围是______________ .
与直线y=a的交点有2个,那么a的取值范围是______________ .