Question

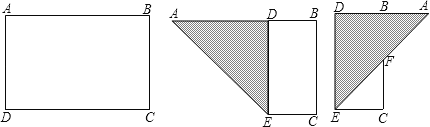
【题目】如图，有一块矩形纸片ABCD，AB=8，AD=6，将纸片折叠，使得AD边落在AB边上，折痕为AE，再将△AED沿DE向右翻折，AE与BC的交点为F，则△CEF的面积为（ ）

A． B． C．2 D．4

Answer 1

【答案】C

【解析】

试题分析：根据折叠的性质，在图②中得到DB=8﹣6=2，∠EAD=45°；在图③中，得到AB=AD﹣DB=6﹣2=4，△ABF为等腰直角三角形，然后根据等腰三角形的性质和矩形的性质得到BF=AB=4，CF=BC﹣BF=6﹣4=2，EC=DB=2，最后根据三角形的面积公式计算即可．

解：∵AB=8，AD=6，纸片折叠，使得AD边落在AB边上，

∴DB=8﹣6=2，∠EAD=45°，

又∵△AED沿DE向右翻折，AE与BC的交点为F，

∴AB=AD﹣DB=6﹣2=4，△ABF为等腰直角三角形，

∴BF=AB=4，

∴CF=BC﹣BF=6﹣4=2，

而EC=DB=2，×2×2=2．

故选：C．