Question

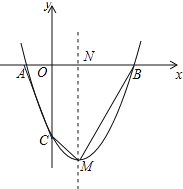
【题目】如图，抛物线y=x2﹣3x+k与x轴交于A、B两点，与y轴交于点C（0，﹣4）．

（1）k= ；

（2）点A的坐标为 ，B的坐标为 ；

（3）设抛物线y=x2﹣3x+k的顶点为M，求四边形ABMC的面积．

Answer 1

【答案】（1）k=﹣4；（2）（﹣1，0），（4，0）；（3）．

【解析】

试题分析：（1）由于抛物线y=x2﹣2x+k与y轴交于点C（0，﹣3），代入解析式中即可求出k；

（2）由y=0，得出方程，解方程即可得出结果；

（3）把抛物线解析式化成顶点式求出顶点M的坐标，四边形ABMC的面积=S△ACN+S△NCM+S△NMB，即可得出结果．

解：（1）把点C（0，﹣4）代入抛物线y=x2﹣3x+k得：k=﹣4，

故答案为：k=﹣4；

（2）∵y=x2﹣3x﹣4，

当y=0时，x2﹣3x﹣4=0，

解得：x=﹣1，或x=4，

∴A（﹣1，0），B（4，0）；

故答案为：（﹣1，0），（4，0）；

（3）∵y=x2﹣3x﹣4=

∴，

设抛物线的对称轴与x轴交于N，如图所示：

则四边形ABMC的面积=S△ACN+S△NCM+S△NMB

=

=

=

∴四边形ABMC的面积是．