题目内容
【题目】如图,直线AB与CD相交于点O,OD平分∠BOE,∠FOD=90°,问OF是∠AOE的平分线吗?请你补充完整小红的解答过程.
探究:
(1)当∠BOE=70°时,
∠BOD=∠DOE=![]() ,
,
∠EOF=90°﹣∠DOE= °,
而∠AOF+∠FOD+∠BOD=180°,
所以∠AOF+∠BOD=180°﹣∠FOD=90°,
所以∠AOF=90°﹣∠BOD= °,
所以∠EOF=∠AOF,OF是∠AOE的平分线.
(2)参考上面(1)的解答过程,请你证明,当∠BOE为任意角度时,OF是∠AOE的平分线.
(3)直接写出与∠AOF互余的所有角.
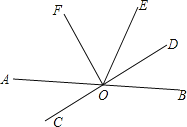
【答案】(1)55;55;(2)见解析;(3)与∠AOF互余的角有:∠AOC,∠BOD,∠DOE.
【解析】
试题分析:(1)根据题意、结合图形填空即可;
(2)根据角平分线的定义和余角的性质证明∠AOF=∠FOE,证明结论;
(3)根据余角的定义解答即可.
解:(1)当∠BOE=70°时,
∠BOD=∠DOE=![]() ,
,
∠EOF=90°﹣∠DOE=55°,
而∠AOF+∠FOD+∠BOD=180°,
所以∠AOF+∠BOD=180°﹣∠FOD=90°,
所以∠AOF=90°﹣∠BOD=55°,
所以∠EOF=∠AOF,OF是∠AOE的平分线,
故答案为:55;55;
(2)∵OD平分∠BOE,
∴∠BOD=∠DOE=![]() ∠BOE,
∠BOE,
∵∠FOD=90°,
∴∠AOF+∠BOD=90°,∠EOF+∠EOD=90°,
∴∠AOF=∠FOE,即OF是∠AOE的平分线;
(3)与∠AOF互余的角有:∠AOC,∠BOD,∠DOE.

 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案【题目】南方A市欲将一批容易变质的水果运往B市销售,若有飞机、火车、汽车三种运输方式,现只选择其中一种,这三种运输方式的主要参考数据如下表所示:
运输工具 | 途中速度(km/h) | 途中费用(元/km) | 装卸费用(元) | 装卸时间 |
飞机 | 200 | 16 | 1000 | 2 |
火车 | 100 | 4 | 2000 | 4 |
汽车 | 50 | 8 | 1000 | 2 |
若这批水果在运输(包括装卸)过程中的损耗为200元/h,记A、B两市间的距离为xkm.
(1)如果用W1、W2、W3分别表示使用飞机、火车、汽车运输时的总支出费用(包括损耗),求W1、W2、W3与x间的关系式;
(2)当x=250时,应采用哪种运输方式,才使运输时的总支出费用最小?
【题目】(2016湖南省邵阳市第12题)学校射击队计划从甲、乙两人中选拔一人参加运动会射击比赛,在选拔过程中,每人射击10次,计算他们的平均成绩及方差如下表:
选手 | 甲 | 乙 |
平均数(环) | 9.5 | 9.5 |
方差 | 0.035 | 0.015 |
请你根据上表中的数据选一人参加比赛,最适合的人选是 .