��Ŀ����
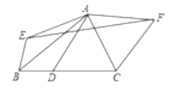
����Ŀ����ͼ��������y=ax2+bx+6����A(6��0)��B(4��6)����y�ύ�ڵ�C��
��1����������ߵĽ���ʽ��
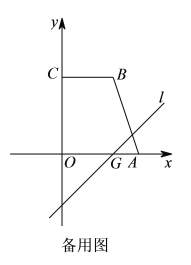
��2����ͼ1��ֱ��l�Ľ���ʽΪy=x�������ߵĶԳ������߶�BC���ڵ�P������P��ֱ��l�Ĵ��ߣ�����Ϊ��H������OP������OPH�������
��3����ͼ1�е�ֱ��y=x����ƽ��4����λ���ȵõ�ֱ��y=x-4����ͼ2��ֱ��y=x-4��x�ύ�ڵ�G����P���ı���ABCO���ϵ�һ�㣬����P�ֱ���x�ᡢֱ��l�Ĵ��ߣ�����ֱ�Ϊ��E��F���Ƿ���ڵ�P��ʹ����P��E��FΪ������������ǵ��������Σ���������ֱ��д����P�����ꣻ�������ڣ���˵��������


���𰸡���1��![]() ��2��S��OPH=8����3���������������ĵ�P����P����Ϊ����0��4��,��
��2��S��OPH=8����3���������������ĵ�P����P����Ϊ����0��4��,��![]() ��
��![]() ��,��4��6��,��
��,��4��6��,��![]() ��6����
��6����
��������
��1����![]() ��
��![]() �������ʽ����⼴�ɣ�
�������ʽ����⼴�ɣ�
��2���ӳ�![]() ��
��![]() ���ڵ�
���ڵ�![]() ����
����![]() ��
��![]() ��Ϊ����ֱ�������Σ�����
��Ϊ����ֱ�������Σ�����![]() ���㼴�ɣ�
���㼴�ɣ�
��3�����ڵ�![]() ������
������![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() �ϣ������������α�����������������ʷֱ���������㼴��.
�ϣ������������α�����������������ʷֱ���������㼴��.
��1����������y=ax2+bx+6����A(6��0)��B(4��6)��
![]()
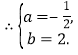 ��
��![]()
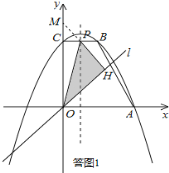
��2���߸������ߵĶԳ���Ϊֱ��![]() ��CP=2��
��CP=2��
��ͼ1���ӳ�HP��y���ڵ�M������OMH����CMP��Ϊ����ֱ�������Σ�
��CM=CP=2��
��OM=OC+CM=6+2=8�� OH=MH=![]()
S��OPH=S��OMH��S��OMP=![]()
��3���������������ĵ�P����P����Ϊ��
��0��4��,��![]() ��
��![]() ��,��4��6��,��
��,��4��6��,��![]() ��6����
��6����