题目内容
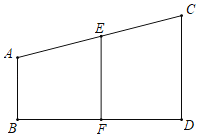
【题目】如图①,△ABC中,AB=AC,∠B、∠C的平分线交于O点,过O点作EF∥BC交AB、AC于E、F.试回答:

(1)图中等腰三角形是 .猜想:EF与BE、CF之间的关系是 .理由:
(2)如图②,若AB≠AC,图中等腰三角形是 .在第(1)问中EF与BE、CF间的关系还存在吗?
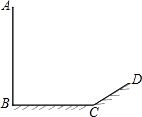
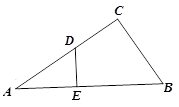
(3)如图③,若△ABC中∠B的平分线BO与三角形外角平分线CO交于O,过O点作OE∥BC交AB于E,交AC于F.这时图中还有等腰三角形吗?EF与BE、CF关系又如何?说明你的理由.
【答案】(1)答案见解析 (2)△EOB、△FOC 存在 (3)答案见解析
【解析】
(1)由AB=AC,可得∠ABC=∠ACB;又已知OB、OC分别平分∠ABC、∠ACB;故∠EBO=∠OBC=∠FCO=∠OCB;根据EF∥BC,可得:∠EOB=∠OBC=∠EBO,∠FOC=∠FCO=∠BCO;由此可得出的等腰三角形有:△AEF、△OEB、△OFC、△OBC、△ABC;
已知了△EOB和△FOC是等腰三角形,则EO=BE,OF=FC,则EF=BE+FC.
(2)由(1)的证明过程可知:在证△OEB、△OFC是等腰三角形的过程中,与AB=AC的条件没有关系,故这两个等腰三角形还成立.所以(1)中得出的EF=BE+FC的结论仍成立.
(3)思路与(2)相同,只不过结果变成了EF=BE-FC.
解:(1)图中是等腰三角形的有:△AEF、△OEB、△OFC、△OBC、△ABC;
EF、BE、FC的关系是EF=BE+FC.理由如下:
∵OB、OC平分∠ABC、∠ACB,
∴∠ABO=∠OBC,∠ACO=∠OCB,
∵EF∥BC,
∴∠EOB=∠OBC=∠EBO,∠FOC=∠OCB=∠FCO,
即EO=EB,FO=FC,
∴EF=EO+OF=BE+CF;
(2)当AB≠AC时,△EOB、△FOC仍为等腰三角形,(1)的结论仍然成立.(证明过程同(1));
(3)△EOB和△FOC仍是等腰三角形,EF=BE-FC.理由如下:
同(1)可证得△EOB是等腰三角形;
∵EO∥BC,
∴∠FOC=∠OCG,
∵OC平分∠ACG,
∴∠ACO=∠FOC=∠OCG,
∴FO=FC,故△FOC是等腰三角形,
∴EF=EO-FO=BE-FC.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案