��Ŀ����
����Ŀ������������ABCD��һ����OΪֱ�Ƕ�������ǰ壬�ƶ����ǰ壬ʹ���ǰ����ֱ�DZ�����ֱ�߷ֱ���ֱ��BC��CD���ڵ�M��N��
��ͼ1������O���A�غϣ����õ��߶�OM��ON�Ĺ�ϵ��
��1���۲���룺��ͼ2������O�������ε����ģ��������Խ��ߵĽ��㣩��OM��ON��������ϵ��___________��
��2��̽��֤������ͼ3������O�������ε��ڲ������߽磩����OM=ON�����ж����ǰ��ƶ��������������������ĵ�O�����ʲôͼ�Σ���˵�����ɣ�
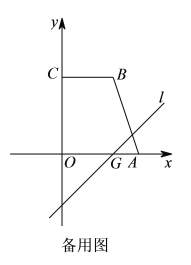
��3����չ���죺����O�������ε��ⲿ����OM=ON��������ͼ4�л�������������һ����������������ǰ��ڸ�������£����ⲿ���ƶ����������������ĵ�O����ɵ�ͼ������д����ȷ�Ľ��ۣ�������˵��




���𰸡���1����ȣ�OM=ON������2���жϣ����ǰ��ƶ��������������������ĵ�O������߶�AC���Խ���AC����֤�������������3�����������
��������
��1������![]() ��
��![]() ����ͨ���ж�
����ͨ���ж�![]() �����Եõ�
�����Եõ�![]() ��
��
��2������![]() ��
��![]() ����
����![]() ������ͨ���ж�
������ͨ���ж�![]() ���ó�
���ó�![]() ���������ֵ�
���������ֵ�![]() ��
��![]() ��ƽ�����ϣ�
��ƽ�����ϣ�
��3����ͼ4���������ã�2�����������ߵķ������ж�������ȫ�Ȳ��ó�����.
��1����ȣ�OM=ON����
��2���жϣ����ǰ��ƶ��������������������ĵ�O������߶�AC���Խ���AC��.
��ͼ3������O�ֱ���OE��BC��OF��CD������ֱ�ΪE��F������OEM=��OFN=90�㣮

���ߡ�C=90�㣬
���EOF=��MON =90��.
���MOE=��NOF��
����MOE����NOF�����ߡ�OEM=��OFN����MOE=��NOF��OM=ON��
���MOE�ա�NOF��AAS��.
��OE=OF��
����OE��BC��OF��CD��
����O����C�Ľ�ƽ������.
�����ǰ��ƶ��������������������ĵ�O������߶�AC���Խ���AC��.
��3����ͼ��ͼ4��
���ǰ��ƶ��������������������ĵ�O�����ֱ��AC�����C����AC��ֱ��ֱ����

 ��������ϵ�д�
��������ϵ�д�